Alterity, Otherness and Nomad Geometries: New Trajectories for the Interpretation of Late Neolithic Monuments

Abstract

This paper focuses upon alterity and how we can more fully embrace intimations of otherness in our dealings with prehistoric monuments. Taking as its inspiration recent attempts to explain such structures, and the landscapes of which they were part, it makes two arguments. First, that while ethnographic analogies offer a vital point of departure for thinking through the possibilities raised by alterity and otherness, we may well have been overlooking a rich set of data—derived from careful excavation and painstaking metrical analyses—that has been sitting in front of us for a very long time. Second, despite over a decade of sustained critical debate, we seem remarkably timid when it comes to seeing where these data might take us. Through the lens of two Late Neolithic stone circles from southern Britain (one big, one small), research into measurement units and alignments is allied with recent excavation and survey data in order to explore ideas of hybridity, nomad-geometry and the arresting/manipulation of time and motion. Placing these glimpses of alterity front and centre, they are then used to establish new starting-points for the interpretation of these structures.

Introduction

This is a discussion about the late Neolithic monuments of southern Britain, and the beliefs about the world and its workings that animated and energized them. Its focus is upon alterity, and the suggestion that while powder may indeed be power, and people may indeed turn in to jaguars, we can also find striking archaeological evidence for past worlds very different to our own in the archaeological data we have spent over a century collecting and exhaustively analysing. The challenge is to bring the otherness that inhabits these datasets to the fore, rather than elide it or explain it away: in short, place it at the very heart of our attempts to account for monumentality as an active and dynamic process. As I hope to demonstrate, while we have been happy to raise alterity as a potentially radical theoretical trajectory for challenging and upsetting comfortable assumptions about past worlds, when it comes to following the interpretative pathways it opens, we have been surprisingly timid. As a rejoinder to this tendency, in the attempt to shed light upon past ontologies and beliefs that follows, rather than focusing on spatial logic (e.g. Landau 2015), attention is instead turned to alterity and what might be thought of as the spatial illogic. By this I mean the glimpses of otherness that lurk in the un-patterned and non-conforming, the uncomfortable and the inconvenient: glimpses that beg to be engaged with on their own terms.

In many ways this discussion offers a concerted attempt to respond to Fowles’ clarion call for the otherness of the past to be brought to light in order to encourage us to think in a more creative way about both past and future (Fowles 2013, 262; see also Alberti et al. 2011, 901). It is also a reaction to Weismantel's plea for the discipline to realize and develop its own perspectivism ‘grounded in archaeological data, methods and questions’ (Weismantel 2015, 142). It was prompted by a growing sense of unease that was brought into sharp focus by a rash of recent studies that sought to explain prehistoric monuments and monumental landscapes. Despite demonstrating considerable ingenuity in the formulation of their arguments, when it came to assembling their final conclusions, each fell back on remarkably well-worn and familiar tropes.

The first of these involved a careful re-appraisal of individual stone positions and axial alignments at Stonehenge in order to argue that the site functioned as a calendar—a means of materializing time (Darvill 2022). In the second, the configuration of monuments within the landscape of the Avebury henge was analysed through astronomical alignments and their emergent relation to movement and procession, in order to reveal an integrated landscape designed to initiate individuals into a complex lunar cosmology through episodic staged procession (Sims 2021). Each of these studies will be touched upon in more detail throughout the course of the discussion. The key point to stress here is that it is not the specific methodologies at work that I want to focus on, but instead the nature of the final interpretations tendered.

Back to alterity. At the level of individual features, deposits and contexts, the recognition of moments of otherness of the kind highlighted by Harris and Robb (2012) has become increasingly commonplace in the narratives we tender (e.g. Banfield 2016). Yet, at the spatial scale of the entire site or landscape, these seem to be elbowed aside by the business of spatial logics and grand, carefully executed plans. As a consequence, instead of difference, we are confronted by a comfortable world of solar/lunar alignments and calendrical calculation: a world that would have been as familiar to the antiquarians of the eighteenth and nineteenth centuries as it is to us today, built as it is on the foundation of spatial logics with tangible historical precedents that make intuitive sense.

Why is this the case? More importantly, is there a way of reconciling these scales and acknowledging the possibility that alterity and otherness might also manifest at the scale of the monument or landscape? To explore this, I will examine the creative spaces and tensions that exist between two well-established approaches to the unravelling of past belief systems and understandings of the world. The first, exemplified by metrical and astronomical studies, assumes that there is a logic underlying (and baked into) the spatial form of a monument or landscape that is a direct reflection of cosmological beliefs and understandings. Decode the template, and by default you shed light on those underlying imperatives (e.g. Hawkins 1973; Landau 2015, 275–6; North 1996). The second draws inspiration from developments within ethnography, anthropology and theology, accompanied by New Materialist and Posthumanist insights into the importance of notions of vibrancy, relationality, flow and emergence. This has inspired a diverse range of studies into the character of religious beliefs and behaviours (e.g. doings); the way in which different ontologies work (e.g. the new animism and perspectivism); and the recurrence of certain motifs and principles (e.g. wrappings and bundlings) (e.g. Fowler 2021; Fowles 2013; Gell 1993; Holbraad 2009; Pauketat 2013; Richards 2013b; Viveiros de Castro 1998). There has also been important work on materiality, performance and memory, highlighting the ubiquity and persistence of deceptively simple ideas and concepts such as circularity and practices such as the raising of stones (Bradley 2005, 113; 2011, 97; 2012; Jones 2012; Richards 2013a). It has also involved vital and productive critique. This has served to foreground the dangers of over-normative, bounded approaches to otherness that risk denying the multiplicity of beliefs and ontological plurality that may have well been in play at any given point in the past. It has also foregrounded the political implications in the present of such perspectives, questioned the uncritical appropriation of indigenous ontologies and highlighted the potential risk that an exclusive (or zealous) focus on alterity can make us blind to the possibility of familiarity (Alberti & Marshall 2009; Alberti et al. 2011; Harris & Cipolla 2017, 185; Harris & Robb 2012).

Bringing them into dialogue

On the one hand, we have the painstaking measurement and numerical analysis of carefully surveyed site plans in order to tease out meaningful quanta and geometries—megalithic yards and high-precision alignments. On the other, we have a range of theoretical studies that have foregrounded alterity as an active concern and highlighted the challenges we face in wielding such insights in a critical and responsible way. Put crudely, the logic that is assumed to sit uncritically at the heart of the former kind of investigation forms the subject matter of the latter. But are they really that different in their ultimate aims?

Although few would now see merit in the purely metrical studies of researchers such as Thom and studies inspired by his work, it can be argued that in their broad aims they had much in common with more recent work carried out as part of the ontological turn. By unlocking the key (or logic) that lay behind the plan form of a given prehistoric monument (whether a standard unit, mode of practical geometry, precise astronomical alignment, or all of the above) they were seeking to understand the ways in which past people understood the workings of their world. That they did so through raw empiricism—insights emerging from meticulous study of the archaeological remains themselves—offers a contrasting, yet potentially complementary, framework to recent explorations that draw more directly upon ethnographic analogy and indigenous ontologies for their inspiration.

In practice two late Neolithic–early Bronze Age monuments in the south of Britain will be used to demonstrate that by bringing these approaches together different, and productive, interpretations are made possible. Both are circles of standing stones thought to date to the late Neolithic or early Bronze Age. One is small and unassuming (Porlock Circle, Somerset), the other large and ever present in accounts of the British Neolithic (Avebury, Wiltshire) (Fig. 1). In each case, the goal is to start to tease out some of the less comfortable or familiar principles that seemingly mattered in the progressive gathering and unfolding of these careful articulations of earth, turf and stone. This is in order to establish new baselines for further interpretation and interrogation of each of these structures.

Figure 1. Location of the sites discussed in the text.

Introducing the monuments

The first example is Porlock Circle, a near-perfect 24 m diameter ring of modest standing stones. Originally thought to have held around 40 megaliths, at present only 19 stones survive (11 upright and 8 recumbent); the largest recumbent is 2 m in maximum dimension, the smallest 0.2 m. The stones that remain standing range in height from 0.08–0.7 m (Fig. 2). Approximately 57 m to the southeast lies a 12 m length of avenue that takes the form of a line of tiny, paired standing stones spaced 0.88 m apart (Gillings 2015a). One of only two stone circles identified on Exmoor, it is part of a group of distinctive megalithic monuments that have been characterized by their strikingly geometric forms—squares, triangles, parallelograms and quincunxes– and the diminutive size of the component stones employed (Gillings et al. 2010) (Fig. 3).

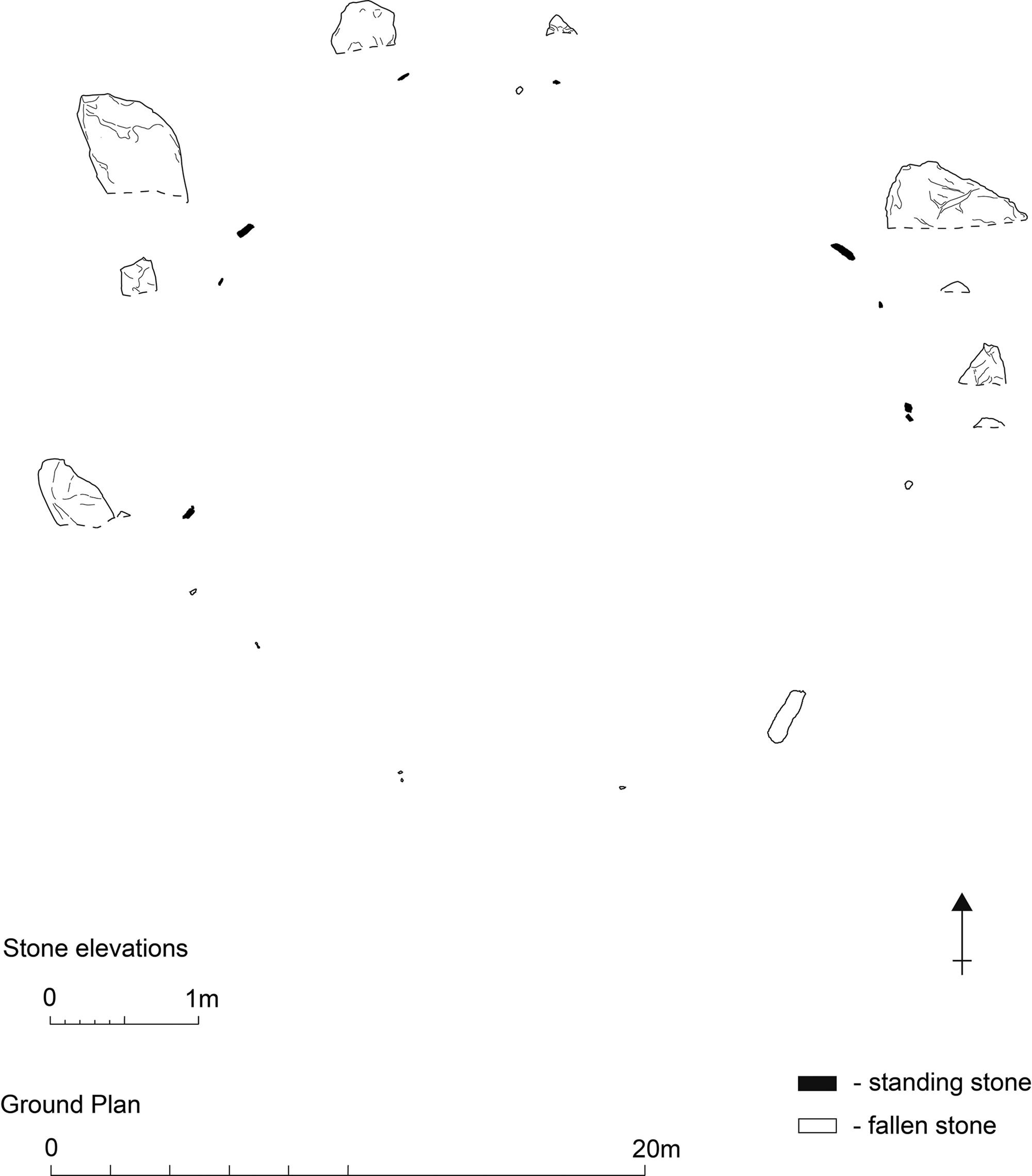
Figure 2. Porlock Circle (plan and stone elevations).

Figure 3. Examples of the geometric stone settings of Exmoor (after Chanter & Worth 1905, pl. IV; 1906, pls III & IV—original measurements converted to metric).

My second example—the Avebury henge—is one of the pre-eminent megalithic monuments of the European Neolithic. Sitting amid a landscape rich in later Neolithic monuments, among them Silbury Hill and the West Kennet palisade enclosures, its 420 m diameter earthwork encloses the world's largest stone circle. This comprises around 98 substantial standing stones that range in height between 2 and 4 m. This in turn encloses two smaller megalithic circles, each around 100 m in diameter with upward of 28 substantial standing stones, which themselves contain further complex stone settings (Fig. 4). From two of its four entrances lead avenues of paired standing stones that together extend for c. 3.5 km to link with other monumental constructions such as the timber and stone circles of the Sanctuary (for detail, see Gillings & Pollard 2004).

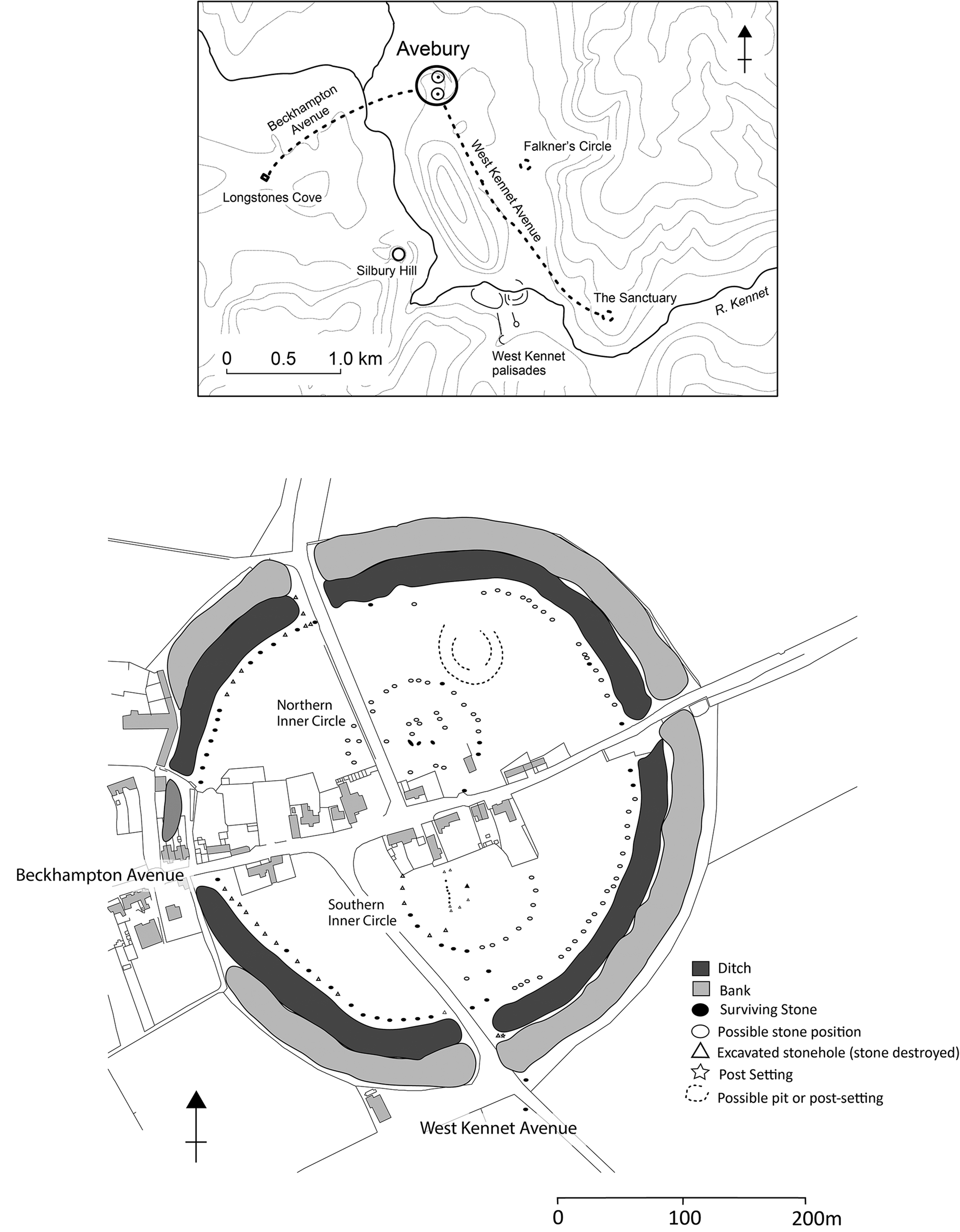
Figure 4. The Avebury henge and its monumental landscape.

Units and alignments

measurement stands at the dawn of cosmology (Renfrew & Morley 2010, 3)

If a trend can be detected in the study of megalithic monuments, it has been to decompose the final plan form of a given structure in order to identify the geometrical principles and standard units of measurement that were deployed in the execution of its design. The assumption is not only that a pattern lurks within the final plan, but that this in turn provides the key that is needed to unlock its singular meaning. This has variously involved attempts to identify the standard quanta (measurement units) employed; for example, Stukeley's ‘Druid Cubits’ (1743, 19–20) and Thom's megalithic yards and rods (1967). It has also prompted complex reconstructions and experiments, alongside more prosaic approaches such as stone counting, in order to tease out the geometrical and numerological principles that guided the ways in which these standard units were deployed (e.g. Thom 1967; Thom & Thom 1978; Burl 1976). Avebury offers a good example. In a suite of studies, the site was used to confirm the validity of the Megalithic Yard and develop the argument that a 3-4-5 triangle (in effect a pre-Pythagorean deployment of Pythagoras’ theorem) was employed in the laying out of stone circles (Thom 1967, 89–91 & frontispiece; Thom & Thom 1978, 30–44). Indeed, it was measurements taken at Avebury that allowed the true length of the Megalithic Yard to be refined from 2.72 ft (0.829056 m) to 2.722 ft (0.8296656 m)—a change of 0.6096 mm—with Avebury ultimately listed as the second (of four) proofs of its reality (Thom et al. 1976; Thom & Thom 1976; Thom & Thom 1978, 41).

the notion of excessive precision has no place in prehistoric numerology. (Chapman 2014, 406)

While explicit interest in megalithic measurement has largely waned in recent years, archaeological and anthropological studies of mathematics and measurement systems have continued apace (e.g. Marchand 2018; Morley & Renfrew 2010). Focusing upon temporal as well as spatial schema, this research has embraced both qualitative and quantitative approaches in an attempt to explore the intimate links that exist between worldviews and how societies measure (Begbie 2010). In an important discussion of practical science in the Mesolithic and Neolithic of central Europe, Chapman (2014) has drawn attention to the significance of dimensional order and ratios in the creation of objects and structures such as houses. This work refocuses attention away from the obsessive concern with metrical precision that has underpinned much work on prehistoric geometrical and measurement systems. What is particularly valuable in Chapman's study is the way in which it loosens the shackles of high-precision measurement schema to consider instead relative dimensions, broad ratios and the character of practical imprecision. As we will see, the issue of spurious precision is particular apposite in the case of Avebury. In their stimulating and persuasive study of late Neolithic measurement units, Chamberlain and Parker Pearson dance between precisions high and low—for example in their study of the early phases of Stonehenge quoting the metric equivalent to their ‘long yard’ to 5 decimal places while simultaneously rounding to the nearest ‘Modular Diameter’ (Chamberlain & Parker Pearson 2007, 171). Recognizing that monuments are often long-lived and their form mutable, the authors argue that any analysis seeking to tease out meaningful quanta needs to focus upon primary construction events. They also make the important point that we should not expect to find universals, with different measurement systems likely to have been employed between areas and even specific monuments. At Avebury a number of recurrent measurements have been noted. For example, the diameter of the Sanctuary stone and timber circle (41 m) appears to correspond broadly to the span of the initial linear setting of three sarsens forming the terminal of the Beckhampton Avenue. It is also mirrored in the stake ring that formed the first phase at Silbury Hill, as well as the platform at its top (Bradley 2000, 107, fig. 32). The consistent appearance of measurements at the Longstones and Sanctuary in multiples of 2.5 m has also led to this being claimed as a possible standard measurement unit (Gillings et al. 2008, 126–8).

Measurements are material-discursive practices of mattering. (Barad 2012, 7)

So far so good, but as Pétursdóttir has noted, instrumental measurements create as much as they reveal (Pétursdóttir 2020, 102). This echoes Barad's arguments regarding the ontological character of measurement, where the act of measuring gives rise to the thing that is notionally being measured (Dolphijn & van der Tuin 2012, 48–70). To use Barad's term, measurements are ‘world-making’ (Barad 2012, 7). Perhaps the most striking example in relation to prehistoric monuments is Hawkins's seminal work on Stonehenge, where pioneering use of an IBM 7090 (‘the machine’) led Hawkins to discover a Neolithic computer (Hawkins 1964; 1965, 99). Perhaps more subtly, it is also evident in more recent studies of the planning, spatial form and geometry of early Neolithic monumental structures and the emergence of geometric architecture (Haklay & Gopher 2020, 1). Although the focus of the latter discussion is with the architectural processes of design and execution—in short, how did the builders achieve the final form—essential to the study is the identification of what the authors refer to as the ‘spatial principles and compositional laws’, logics and rules that shaped the final monument (Haklay & Gopher 2020, 5). In a further illustration of Barad's dictum, it is perhaps not surprising that, having approached the monument through the lens of quantitative, formal architectural analysis, the authors find clear evidence of formal, geometric architectural planning (Haklay & Gopher 2020, 10). We might also note the study by Case (2004) seeking to use an assumed set of underlying geometric principles and shapes (in this case circles, triangles, squares and hexagons) in order to be able to reverse engineer the constructional sequences of a range of circular prehistoric monuments. On Exmoor, the assumption that its megalithic monuments adopted rigidly geometrical forms has certainly coloured decisions as to which particular stones to include/exclude when recording and reconstructing these fragile settings (Gillings et al. 2010). It is not only the monuments that can end up circular in such studies.

Accompanying this research into standard units and mathematical principles has been an active interest in axes and alignments. This has been used to argue for the importance of often complex astronomical schema as well as reflecting deep, underlying structures. Take, for example, Darvill's analysis of the changing meanings of Stonehenge. His argument was that the existence of an initial axis reflected an underlying cosmology of binary opposition, an axis derived from the landscape itself and its earlier history. Between c. 2900 and 2400 bc this was reworked with two non-perpendicular axes—a primary axis sighted on the midsummer sunrise and a ‘secondary’ axis crossing it at 80 degrees. These axes projected out from the monument, dividing the landscape into four sectors—what Darvill termed a ‘linear quadruple partitioning of space’ (Darvill 1997, 186) once again reflecting an underlying cosmology of binary opposition. What is interesting is that Darvill suggests that this four-fold space is reflected not only in the monument itself, but the decoration found on artefacts such as chalk plaques and beakers. By the later third millennium this quartering was initially elaborated and then superseded by the principle of concentricity, as seen in the stone and timber settings at monuments such as Woodhenge and Durrington Walls, as well as Stonehenge itself. Once again, this is argued to be reflected in contemporary decorative schema (Darvill 1997, 181–91). There are undoubtedly issues with Darvill's scheme. The phasing assumptions that underlie it can be criticized (Pollard & Ruggles 2001, 74) and it arguably falls into the trap of much structuralist-inspired work in assuming that the hard work stops with the list of specific binary oppositions being invoked as deep organizing principles. There is also the explanatory displacement issue; if Stonehenge's cosmological axis was inspired by the earlier history of the landscape, where had the binary oppositions that seemingly animated that earlier history themselves come from? Despite this, it is to be commended for the attempt it makes to move beyond description to consider questions of Neolithic ontology and epistemology. The importance it places upon partitioning and the potential significance of the number four is also significant and a point to which I will return.

As with the privileging of measurement units, a focus upon alignment also has consequences. In the case of circular sites (that can effectively point anywhere), this has resulted in a near fetishization of distinctive structural elements, such as recumbent stones, earthwork notches and entrances as the only elements that can be confidently lined up. Studies that emphasize significant axes and orientations also tend to be based upon the plan form of a given structure and are predicated on the assumption that this is the result of careful and deliberate design (the spatial logic discussed earlier). Even when acknowledgement is made of a long history of activity at a given site, there is still the assumption that the discrete phases identified were the result of conscious planning. Take, for example, the reading of phase changes at Stonehenge noted above (Darvill 1997).

This packaged, stop-start understanding of monuments and the landscapes of which they are part has long been challenged by works that have emphasized the importance of on-going processes of modification, assemblage and citation in the progressive emergence of such structures (Jones 2012). It has also been questioned by the results of detailed excavation that have stressed the often long and complex histories that underpin what appear to be fixed and immutable typological forms (e.g. Bradley 2011). This is not to argue that axes and alignments may not have been significant, merely to point out that the interpretative tactic of arresting the flow and flux of a long-lived monumental structure in order to identify (or distil out) a claimed alignment requires careful critical reflection. The question must also be asked as to whether the axial alignments should form the dominant focus of enquiry as opposed to the partitions they generate. To use the analogy of a field-system, by focusing solely on the hedgerows, do we risk forgetting the significance of the fields that lie to either side? Could it be that the significance of such axes lies less with what they represent or point at, and more with what they do? I will return to this issue shortly.

Why does familiarity always trump otherness?

Perhaps the most striking feature of current disciplinary attempts to shed light on prehistoric cosmology is the prosaic nature of the interpretations being tendered. There is certainly no evidence here of any blindness to the possibility of familiarity. For example, through the careful counting of stones and mapping of meaningful alignments, Stonehenge has moved from being a calendar (Lockyer 1909), to a calculating device (Hawkins 1965), to a calendar again (Darvill 2022). This rediscovery is then used to posit and reinforce the notion of a solar cult/cosmology that potentially emerged (lux-like) from the east. What is interesting here is the inherent denial of otherness that is needed in order to allow the site to work in this way. The result is a mechanism that makes intuitive sense, with little in the way of alterity on display, whether writ large or else manifesting as an unusual/awkward/unsettling moment in an otherwise familiar setting. Like Hawkins's computer, the calendar has a single job and does it well. What is more, following Hutton, it is suggested that the reason this underlying cosmological system is so immediate and recognizable is due to the remarkable survival to the present day of much earlier beliefs and practices. It is familiar to us because it has never really gone away. Such calls risk blinding us to the possibility of unfamiliarity and are worthy of study in their own right. To that end we might highlight Hutton's musing that as interesting as the possibility that beliefs and practices from deep time survive intact into the present is the question as to why so many people have been willing to believe that they did (Hutton 1996, 425).

The assumption that the final form of a monument, or indeed landscape, encodes a singular mystery—and a cosmological one to boot—is clearly a pervasive one. As noted, in such studies the archaeological challenge is to find the key, and when this is carried out at a landscape scale that process invariably has to operate at a high level of generality in order to work. Any complexity is reserved for the explanatory gymnastics that are required to explain away seeming contradictions or tensions, rather than in the careful reading of the fine-grained archaeological detail where much of the otherness can be found. Take, for example, the significant astronomical alignments argued for the Avebury henge (Sims 2021, after North 1996). Here the configuration of the monuments within the landscape is argued to have served as a model of the underworld designed to structure rituals linked to cycles of the moon. This is a landscape that aligns with the cosmos; part initiation-engine and part cosmogram (Fowler 2021).

Needless to say, if you are looking for meaningful alignments, the sheer density of points to ‘join up’ in the architecture of a site such as Avebury (not least the c. 160+ substantial megaliths) means you are highly likely to find them (Barad again). Interestingly, where we actually have archaeologically attested linear features of three or more elements (e.g. Gillings et al. 2017), none correspond to the astronomical sightlines proposed by Sims (Fig. 5). Indeed, rather than follow the archaeology, the archaeology is made to follow the explanatory schema that is then retro-fitted to it (Sims 2009; 2021, 109): circles within circles. While there is explicit talk of ontology, the focus here is once again epistemological—unlocking late Neolithic ways of encoding and exploiting the cyclical movements of the heavenly bodies or transition of the seasons. In this sense the archaeo prefix of the archaeo-astronomy being touted is redundant (Sims 2021, 129). In much the same way that this ensures that Stonehenge remains the same kind of calendar (albeit more complex) as it was for Lockyer, the Avebury complex remains the same kind of cosmogram/lunar/solar temple (albeit more complex) as it was for William Stukeley in the early eighteenth century and Michael Dames in the twentieth (Dames 1977; Gillings & Pollard 2004, 156).

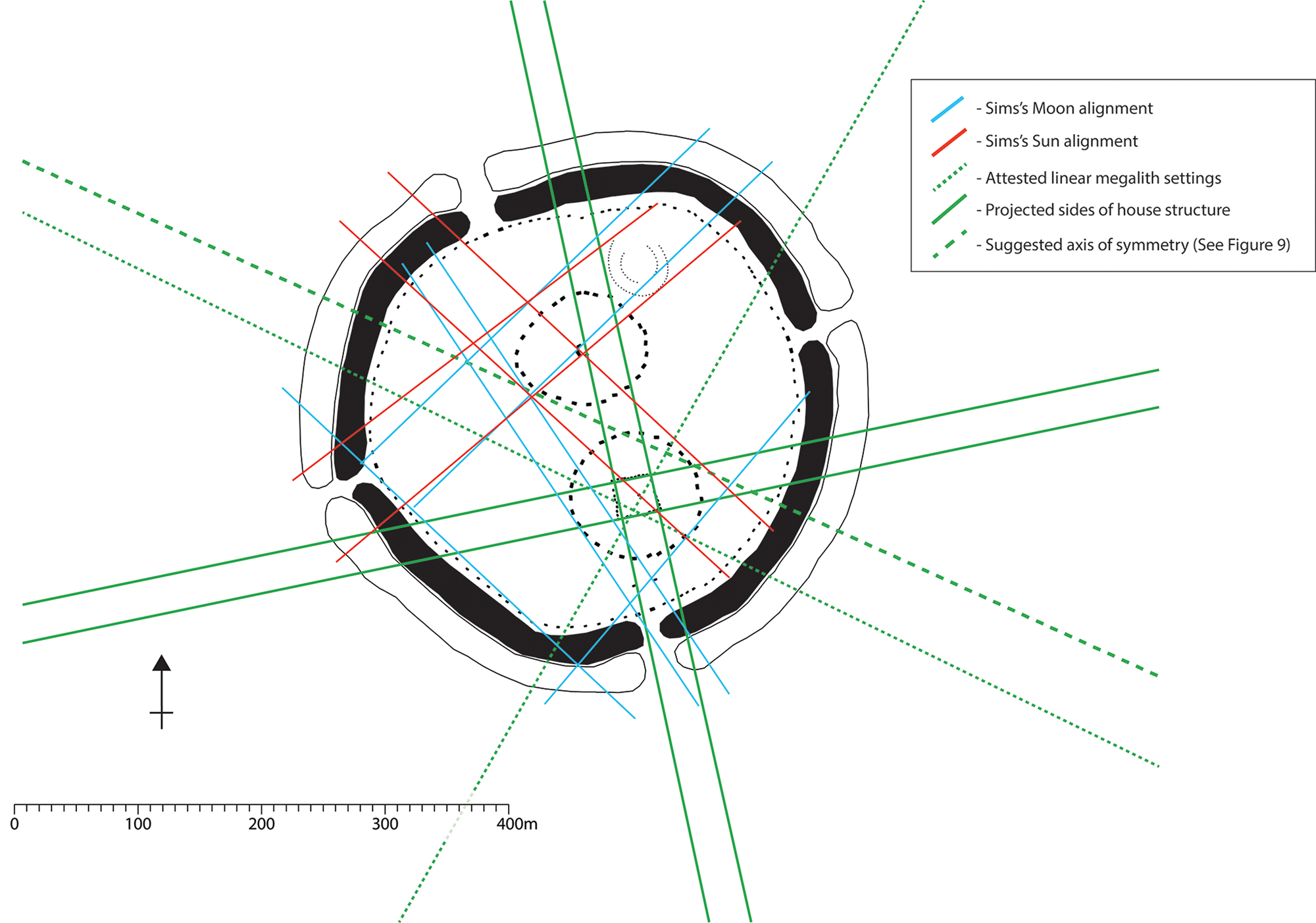
Figure 5. The proposed solar and lunar alignments at Avebury (Sims 2021) alongside the projected axes of archaeologically attested linear settings of standing stones.

These studies offer at best a form of alterity-light, insofar as they are not really acknowledging ontological otherness in any meaningful way at all, more a slightly skewed manifestation of the familiar. Their concern is with epistemology (different ways of making sense or quantifying recognizable periodicities and behaviours of our world) rather than ontology (glimpses of a radically different world). Sites like Stonehenge and Avebury will always be observatories, calculators, calendars or almanacs if that is the sole range of options allowed. Rather than scour monuments and monumental landscapes for meaningful alignments that fit the particular interpretative template we have elected to apply—as a reckoner of this, or a machine to calculate that—what happens if we instead allow their alterity to surface and begin to work with that?

Back to Porlock Circle

With the above discussion firmly in mind, we can now return to the examples sketched at the beginning of the discussion. While the rigid geometric forms taken by the Exmoor monuments have been woven deeply into at least one interpretation that has been tendered for these megaliths (Tilley 2010), what is perhaps most striking is less their fixity and more their flexibility as a form of architecture (Gillings 2015b). Excavation has demonstrated that in many cases the small stones that made up the individual settings were designed to go up and down, and that the forms which survive today may represent a frozen moment in an ongoing process of selection and decision-making as to which stone to raise and which to rest, rather than a timeless monumental statement. Sometimes the result was a particular geometric form that has resonance (square, rectangle, triangle) but sometimes it was not (those deemed today to be incomplete or random). Nowhere is this illusion of fixity more apparent than in the perfect circle at Porlock. Today the surviving standing stones sit at all angles, including stones assumed to have fallen to lie flat on the ground (Fig. 6). Some of the stones stand proud of the turf, while others are so small they barely protrude at all. Excavation of part of the circuit revealed that this rather higgledy-piggledy setting was not the consequence of millennia of impacts and disturbances, but had been intended from the start. The stones that barely protruded above the ground surface were neither broken nor disturbed. Instead, they had been deeply set in order to ensure that only the very top protruded. They were essentially upside-down: likewise the one tilting stone that has been excavated. This had been carefully inserted into a sloping stone-hole that guaranteed that the resultant megalith would lean. When we combine this with the stones lying flat, a different kind of monument begins to impress itself upon us. The idea that this reflects a simple binary has already been rehearsed (Gillings 2015c). Here we have two circles meshing together within a single circuit—one comprising stones that reach up, the other with megaliths that reach down. A ring of uprights interdigitated with its direct opposite. There has been recent interest in inversion as a marked Bronze Age practice linked to a range of structures and practices associated with death and burial (Wiseman et al. 2021). It is also implicit in the case of the inverted oak tree placed at the centre of the Bronze Age Holme 1 timber circle (Groves 2002). The suggestion is of two worlds meeting at the surface of the ground, and the stones of Porlock Stone Circle can certainly be read in this way. Although the dating of Porlock Circle to the late Neolithic is by analogy only, this also suggests that this Bronze Age phenomenon may have been building upon much earlier roots.

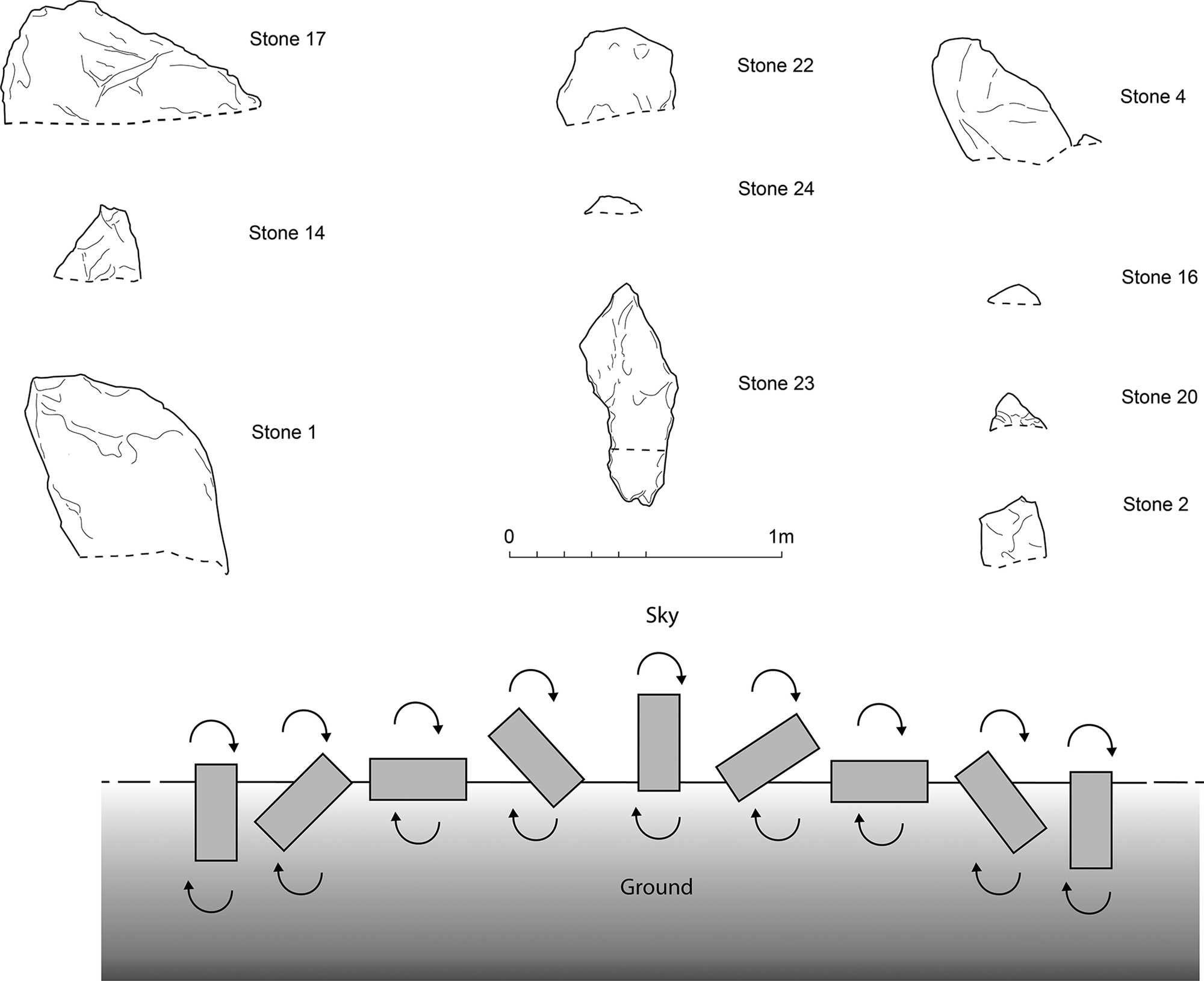
Figure 6. Examples of stone elevations at Porlock Circle alongside an abstract representation of the arrested tumbling of stones.

While this explanation is undoubtedly neat, does it really do justice to the complexity, and more importantly alterity, of what seems to be taking place at Porlock Circle? What about the stones that are deliberately leaning and lying flat? We can see these as transition states between the up and down. Rather than reflecting and embodying fixed states (Skywards/Chthonic) they are instead serving to capture, or arrest, entities in process; megaliths that are dynamically pivoting or revolving around the point at which stone and earth meet (Fig. 6). Imagine each component stone is itself endlessly spinning. If each began its cycle a heartbeat after its neighbour, the circle itself would effectively spin. If the pivoting of the component stones was instead unrelated, the effect would be a chaotic boiling. The circle is composed of stones defining their own circles, an out-of-phase tumbling; a never-ending progression or vibrant churning, that would in turn animate the ring itself (Figs 7 & 8. See also supplementary material). Like the seemingly geometric stone settings that punctuate Exmoor's landscape, Porlock Circle is another example of a frozen moment, but far less negotiated and as a result less contemplative. Rather than selecting stones to raise or lower in order to mark or inscribe, Porlock Circle is a structure that has been captured in the process of blurring and thrashing; a monumental doing being held in its tracks: potential energy.

Figure 7. How does one represent (capture) the dynamic nature of a site like Porlock Circle? In the first of two experiments, a scale reconstruction was created using windmills (pinwheels) as standing stones. A tape was swung around a central point to inscribe the arc of the circle and holes were drilled in order to plant the windmills. Once constructed the wind was then left to rotate the windmills and bring the circle to life. Changing wind patterns and eddies served to spin some of the windmills while stilling others in an often haphazard, unpredictable fashion. While the digital possibilities of visualizing a monument in motion are endless, the decision to engage a more performative analogue methodology here was deliberate. A short film recording of the process has been included in the supplementary online material.

Figure 8. How does one represent (capture) the dynamic nature of a site like Porlock Circle? In the second experiment, a series of progressively tilting cardboard megaliths were attached to a horizontally mounted bicycle wheel using duct tape. In deciding on the size of stones, scale was exaggerated for clarity. Once constructed, the wheel was spun in order to bring the circle to life. Functioning as a crude zoetrope, when viewed from the side the sequential tumbling of the stones became apparent. Once again, while this could have been achieved digitally, the analogue method adopted allowed the process of making and performance to be directly experienced. A short film recording of the process has been included in the supplementary online material.

Back to Avebury

In the case of Avebury we are fortunate insofar as work has already been under way to foreground and explore manifestations of alterity, inspired in large part by the ethnographic works noted earlier. This has explored questions of stone animacy and agency (e.g. Pollard & Gillings 1998) as well as begun to tease out the new explanatory pathways that emerge when we stress the transformative flows of substances, capacities and energies involved in the movement and raising of megaliths (Gillings & Pollard 2016). Important work has also been carried out on approaching the individual stones that make up the monument not as static components, but instead animate material assemblages (Banfied 2016). There is nothing timeless, fixed and enduring about Avebury and never was. A restlessness and fidgety indeterminacy characterize what can best be described as a remarkably energetic structure. Take, for example, the precipitously steep cut of Avebury's ditch, which appears to have been deliberately effected in order to accelerate and amplify decay and erosional change (Ashbee 2004). Something pristine and new quickly became something old, slumped and weathered: accelerated ruination. This had the twofold impact of simultaneously speeding up the passage of time (Avebury aged too quickly) while telescoping the past into the present. There is also the question of the stones themselves, dragged from their original positions into wholly new configurations and fixed into place in an attempt to stop them from ever returning; a bottling and frustration of movement, a binding into place. Movement arrested: perhaps another manifestation of the kind of dynamic stationarity evident at Porlock Circle. To repeat, there is nothing timeless and enduring about this monument, and it may not have been alone. Much the same has been argued for the site of the Sanctuary, a timber and stone circle linked to the main Avebury monument by the West Kennet Avenue. Here the repeated removal and replacement of timber uprights led the excavator to describe it as a monument-in-motion: always changing and never still (Pitts 2001).

Practical imprecision

While Avebury has proven a frustration to archaeoastronomers, beyond some rather tenuous links to the star Deneb (Thom & Thom 1976, 191; Thom & Thom 1978, 40), I have already noted how the site was critical to the refinement and ‘proof’ of the Megalithic Yard. It is also a circular site whose investigation and interpretation have been very much shaped by its four entrances and lines projected between them. Put simply, it is very much a monument of quadrants (Smith 1965). But as stone circles go, Avebury is a curious structure. Despite the best efforts of William Stukeley (see for example his famous frontispiece to the Abury volume of 1743), Avebury presents a poor model of circularity, and its quadrants are anything but equal. The irregularity of the bounding earthwork and outer stone circle has long been noted and retrospectively apologized for, explained away as an unavoidable consequence of the scale and mode of construction (e.g. gang-built in an episodic fashion and/or the sheer difficulty of laying out a perfect circle of this scale across a raised ridge of ground). Its irregularity has also been seen as largely irrelevant, the importance of views out from the monument trumping any concern with its final plan (Gillings & Pollard 2004, 7). But it can be argued that the noted irregularity of Avebury's earthwork and outer circle are simply a legacy of the tendency to structure interpretation around assumptions of perfect circularity and regularity in the placement of entrances. If we ignore these, then while the final-phase Avebury earthwork may not be circular, it does have a distinctive shape and it does demonstrate remarkably strong levels of bifacial symmetry (Fig. 9). Key to this are the peculiar ‘corners’ evident in the first archaeological plan of the site drawn by John Aubrey in 1663 and first noted by Alexander Thom; the consequence, he argued, of the two intersecting geometries needed to create its distorted form (Thom et al. 1976, 184–5).

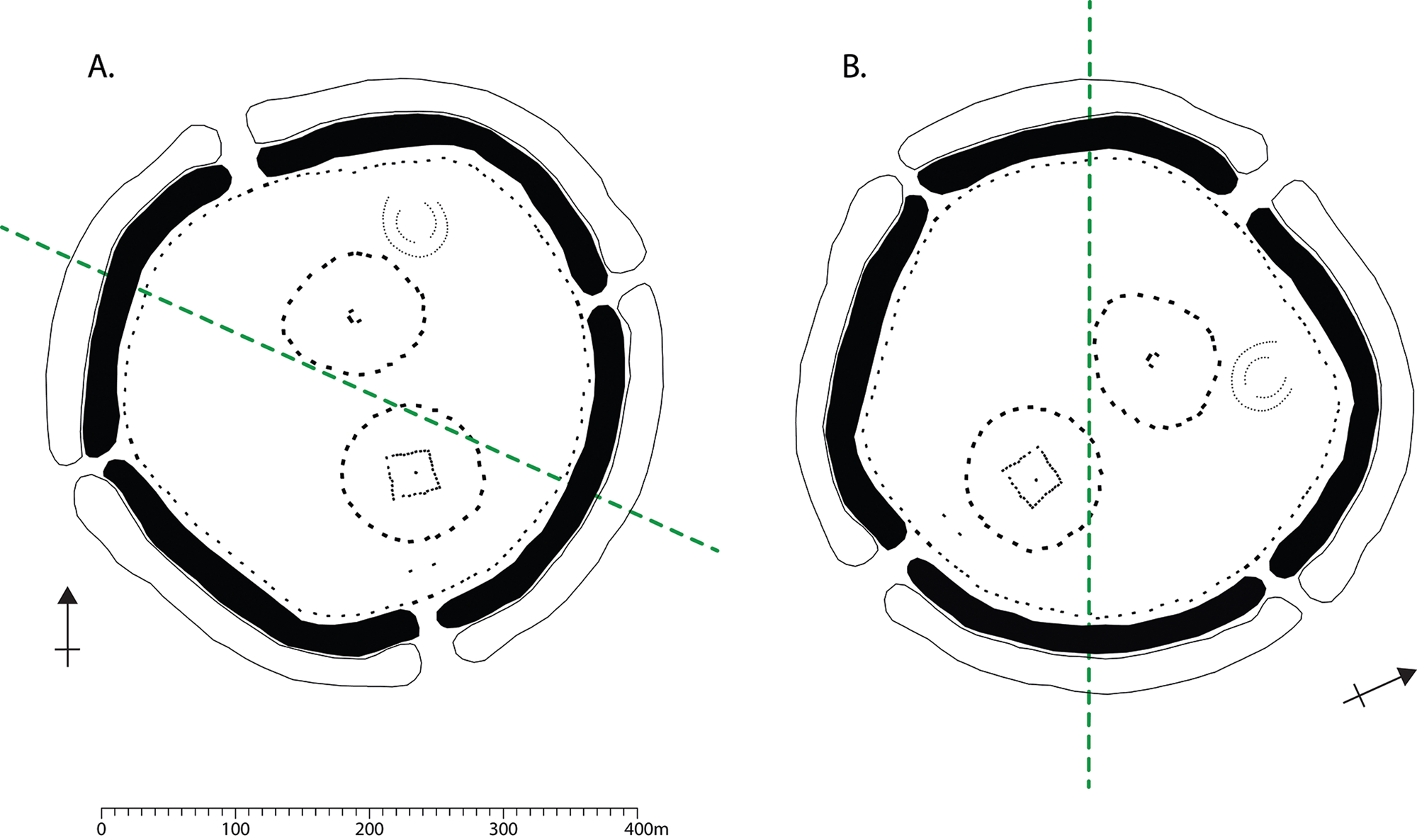
Figure 9. An axis of symmetry at Avebury (A). To make this visually clearer, it has been rotated to the vertical (B). As the placement of the inner circles suggests, this may be only one of many meaningful axes (folds) present at the site.

Folds, mirrors and reflections

a body is that which folds (Forsythe in Dolphijn 2021, 122)

Imagine approaching Figure 5 through the lens of origami instead of celestial alignment (Figs 10 & 11). If we focus not on what this axis aligns with or points towards, but instead on what it does, it acts first and foremost as a fold (Aedo 2018). This fold in turn engenders mirroring or reflection, a phenomenon also evident in the pairing of the northern and southern inner circles, where once again the axis around which this reflection is articulated is perhaps less significant than the mirroring it facilitates. This focus on the fold is all well and good, but it does raise two vital questions that need to be addressed. The first is whether that is all that a fold can do—create an axis for mirroring, and no more? Second, as should be clear from Figures 10 and 11, this focus on folding is predicated upon the plan form of Avebury, which in turn requires a detached, all-seeing viewpoint in order to identify and execute the folds it would like to make—Haraway's ‘conquering gaze from nowhere’ (Haraway 1991, 188). How can a monument be folded ‘on the ground’?

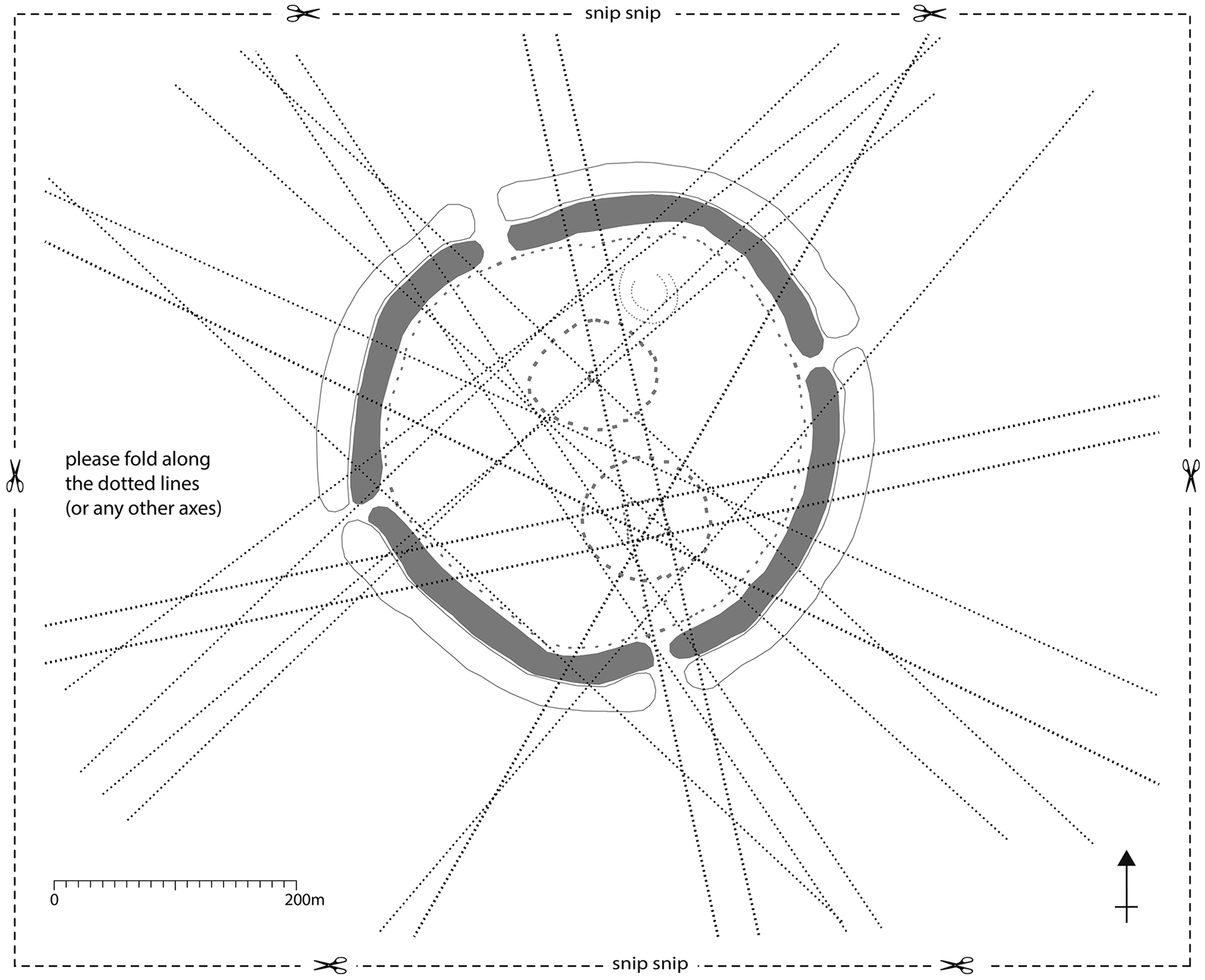
Figure 10. The reader is invited to grab a pair of scissors, take hold of Avebury and begin the process of folding. Think about the changed configurations and emerging topologies as creases are made. Also experiment with ignoring the dotted lines to explore other potential axes and lines of fold.

Figure 11. The process begun in Figure 10 need not end at the boundary of the monument. Here the dotted lines have been extended into the wider monumental landscape—the structure to the northwest of Avebury is the early Neolithic causewayed enclosure of Windmill Hill.

Here I would like to draw upon Dolphijn's examination of the dialogue between Massumi and Forsythe on the distinctions between modernist and contemporary dance (Dolphijn 2021, 122–30). Critical to the arguments developed is the idea that rather than bodies dancing, dancing instead serves to body, with the fold the vital act through which such bodying is effected. As Dolphijn notes, ‘it is only through the act of folding (the dance) that it (the body) realizes itself’ (Dolphijn 2021, 123). Might the same be true of monuments? Enough people engaged in the act of folding can in turn fold anything: a complex and breathless choreography giving rise to new topologies, new configurations and new monuments. And the performance of every fold in turn gives rise to creases and scores, scuffs and pathways, striations that in time will criss-cross and texture the gaps between the upstanding stones. Indeed, when you finished exploring the folds made possible in Figures 10 and 11, try to flatten out the sheet and consider the wrinkles you are left with.

Building on the above, we can also look at the standing stones themselves. Rather than interpret them as neutral building materials, ciphers or representations (e.g. their resemblance to crude male/female archetypes, faces or animals) we can extend the metaphor in a grounded way and treat them as participants in the dance: bodies that are happening and realizing themselves through the folds they enact. Once again, the evidence is there if we allow ourselves to see it. There are stones that appear to have been frozen in-the-process-of-folding (e.g. Fig. 12). Others bend at the waist to lean, such as Stone 2 of the Avebury Cove (Gillings & Pollard 2015).

Figure 12. A folding stone at Avebury.

On the basis of current evidence, the final-phase earthwork follows the precise circuit of a much earlier bank and ditch (whose own entrances are unknown). Likewise, the inner circles may have been some of the earliest stone settings at the site (see Gillings et al. 2008; 2019) which suggests that this folding and reflection appear to have been cooked into the monument from the outset. This once again argues that the principles of mirroring argued to have been a Bronze Age preoccupation may well have had much earlier origins, and it is important to remember that polished metal mirrors are only one source of reflection. For example, on-going palaeoenvironmental research on the line of the West Kennet Avenue at Avebury has highlighted the possibility that for significant periods of the year the paired line of standing stones ran alongside a series of stepped pools of standing water (M. Allen, pers. comm. 2017): perfect mirrors. Reflection in turn implies bipartite division, and sidedness (left/right) is evident in Phases 1 and 2 at Stonehenge and has been argued to be a recurrent feature of artefact deposition in late Neolithic monuments. Indeed, the strength of this association was sufficient for Pollard and Ruggles (2001, 80–81). to argue for the existence of meaningful cosmological divisions into halves and quarters.

The sign of the four?

‘Come, Watson, come!’ he cried. ‘The game is afoot.’ (Conan Doyle [1904] 1981, 636)

As for meaningful quanta, if we follow Chapman and relax any commitment to precision, then we find persuasive support at Avebury for Darvill's suggestion that four may have been a significant number. At the heart of the southern inner circle are the remains of an early Neolithic house—a square timber structure c. 7 m in maximum dimension (Gillings et al. 2019). Surrounding this structure is a square setting of megaliths c. 30 m across that respects the orientation and position of the house—an explosion or exaggeration of its footprint. This sits within the wrapping of an approximately 100 m diameter circle of standing stones (the southern inner circle) that itself sits within the outer stone circle and earthwork (diameter c. 420 m). The combination of a square structure set centrally within a circle has been recognized as a distinctive type of what Pollard has termed sacred architecture—the square-in-circle (Pollard 2010, 341–4). Building on the seeming ubiquity of this motif, Darvill has drawn a metaphorical link between circles and the untamed/wild (what Deleuze and Guattari might term smooth) and squares the ordered/stable (striated), the square-in-circle in turn serving as a metaphor for the wild enclosing the domestic (Darvill 2016, 100 & 104; Bonta & Protevi 2004, 143–55).

The quoted measurements above are estimates by necessity, because of the partial and fragmented survival of the monumental fabric. However, as will be seen, precision is a secondary concern in the argument being developed. By analogy with other house structures, the timber structure at the heart of the southern inner circle appears to be the starting point. Inspired by notions of concentricity and wrapping, in the original report a simple and progressive inside-out scheme was proposed; the house enclosed by the square, which was enclosed by the circle, which was enclosed by the outer circle (Gillings et al. 2019): ripples on the surface of a pond. Another reading is possible. The ratio between the maximum dimension of the early house (c. 7 m) and its exploded megalithic representation (c. 30 m) is 4.28:1. Likewise, the ratio between the southern inner circle (c. 100 m) and the outer circle (c. 420 m)—4.2:1. Given the stated ambiguities in measurement and repeated caveats regarding spurious precision, let us simplify this to 4:1. Returning to the question of phasing, if we think instead of squares-in-circles, we can envisage a situation where the original house was enclosed by the southern inner circle. When the house was effectively quadrupled in size to create the megalithic square, it too was enclosed by a similarly exploded circuit, Avebury's outer circle and earthwork (Fig. 13). Although the precise configuration of structures and settings that make up the northern inner circle is very poorly understood (and undoubtedly complex), there are hints that a similar process of expanding squares and circles may also have been taking place there—another instance of mirroring and reflection.

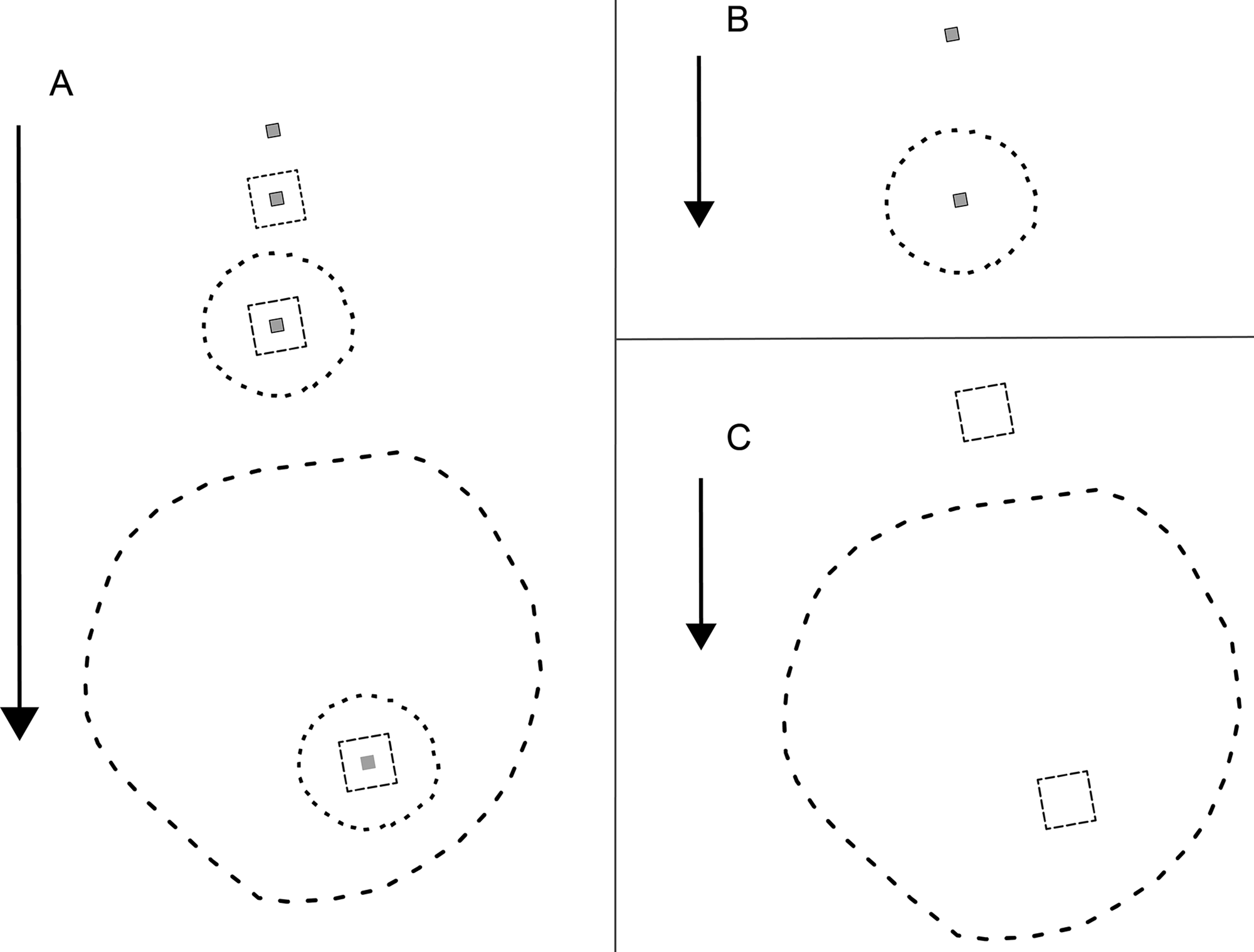
Figure 13. A schematic representation of alternative developmental sequences for the southern inner circle at Avebury (NB: not drawn to scale). In (A) is the progressive ‘wrapped’ sequence presented by Gillings et al. (2019). If we focus on a four-fold ratio, a different trajectory is possible. In step 1 (B), the original house footprint is surrounded by the southern inner circle. In step 2 (C), the exploded house footprint is in turn enclosed by the outer circle.

What I would like to extract from the above is the significance not of alignments, but of folds, reflections, creative play between square and circular forms and the number four in the emergence of Avebury as a monumental complex during the later Neolithic. This not only found expression through dimensional order and ratios but was echoed in the number of sides and corners of the various elements—the house structure, the megalithic re-statement of this, the stones of the Avebury Cove. It is also there in the final-phase earthwork entrances, the latter emphasized by the huge outer circle stones that bracket them. At this point it could be countered that the conclusions being drawn are themselves based on very selective foundations. Having decided that four may have been a significant number, ratio or quantity, all I have done is to sift the evidence to find expressions of it. Such a criticism is fair, and it is undoubtedly the case that there are ratios, counts and dimensions at Avebury that have little or nothing to do with any quadruple multiplier or factor. However, a dominant four-fold mode of expression is present in other elements of the monument complex, such as the Sanctuary with its four symmetrical sections separated by aisles (Pollard 1992) and the megalithic box defined by the stones of the Longstones Cove (Gillings et al. 2008). It is also worth stressing that Avebury is one of only four henge-enclosures, together with Durrington Walls, Mount Pleasant and Marden (Harding 2003, 9-11). Ever mindful of Chamberlain and Parker Pearson's warning that we should not expect any observed measurement quanta or principles to have applicability beyond a specific monument or regional context, there are also hints that complex interplays between squares and circles and the sign of the four may have had broader currency. We have already discussed Darvill's ‘linear quadruple partitioning’ at Stonehenge, and at Site IV at Mount Pleasant a 38 m diameter set of concentric timber circles were divided into four regular quadrants through distinctive corridors (Wainwright 1979, 22, fig. 7). The post rings were subsequently replaced by a 6 m square setting of megaliths and pits, sharing the alignment of the earlier corridors (Wainwright 1979, 28, fig. 16). Rather than radiating out, the fourfold schema was here condensed and concentrated. In his radix analysis of the stone counts making up the circles of the British Isles—a careful attempt to evaluate the high-precision claims of researchers such as Thom—Burl tentatively suggested that either four or six might have served as the base values of a counting system in Neolithic Wessex (Burl 1976, 25–9, tables 9 & 10). Ranging more broadly, Bradley has drawn attention to the recurrence of multiples of 12 in stone counts at the early Bronze Age Clava cairn at Balnuaran, northern Scotland (see also Burl 1976) and the four-fold multiplier that obtains between the number of kerbstones around the cairn and orthostats of the passage and chamber (Bradley 2000, 46; 2012, 104–5).

A circle with corners

What does geometry measure? For by its name and title, it claims to measure an earth. Which one? (Serres [1995] 2017, xiii)

This is the only ring known to us which consists of circular arcs meeting at an angle instead of running smoothly into one another. It thus has what might be called corners. (Thom et al. 1976, 184–5)

While a sacred geometry is floated for the Avebury monuments in the work of researchers such as Sims, it is very much ‘our’ geometry (i.e. that of the classical world) and there is little consideration that other geometries might also have existed whose manifestations we are less able to identify readily. Key to this is the observation of Thom et al. that Avebury comprises a circle with corners, which in turn raises the possibility that we are seeing a very different manifestation of the square-in-circle imperative noted earlier: a quite literal square-in-circle. The line traced by the earthwork circuit embodies aspects of both circle and square. The question is how to view this. We could regard it as deliberately embodying, in a Janus-like fashion, separate (yet distinct) qualities of squareness or circularity that might manifest in response to different contexts or viewing positions. This is Avebury as chimera—Thom's circle with corners—a complex beast for sure, but one whose component elements were distinct and recognizable, allowing the whole to be decomposed into its constituent (meaningful) parts. More challenging—yet productive—is to see the earthwork instead as a hybrid, a combination resulting in something distinctive and not readily reducible to its component parts: in this case a different kind of geometrical figure that hints at a different kind of underlying geometry. That this concern with hybridity may have had early origins is hinted at in other contexts in the wider landscape, for example in the placement and fusion of animal and human bones at Windmill Hill (Whittle et al. 1999, 204–6). As noted, while the main earthwork at Avebury appears to date to the later Neolithic (2600 bc), it seems to have followed closely a smaller, primary-phase earthwork that has been tentatively dated to around 3000 bc (Pollard & Cleal 2004, 124–5). This suggests that this geometric form predated by several centuries the arcs of stone set around its inner perimeter.

The distinction between chimera and hybrid is an important one. If the key to unravelling Avebury's ground plan lies with folds and hybridity, then at the very least we need to expand our explanatory vocabulary of archetypes—squares, circles and lines—accordingly. It also encourages us to question and rethink the schema we use to explain away irregularity in the geometric forms we expect—as an accident caused by poor planning or unavoidable consequence of episodic gang-digging, for example. What if it is exactly what it was intended to be? What if it is instead a very successful inscription of a geometric figure we simply have no words for, and as a consequence have trouble seeing? Might the same be true of the stone settings of Exmoor deemed random or incomplete? Avebury as hybrid (square-in-circle) invites us to consider the possibility of a different kind of geometry—a more nomad, vagabond geometry that prioritizes flow, flux and heterogeneity instead of rigid and stable forms (Deleuze & Guattari 1988, 361–74). It also collapses modernist dualities such as wild:domestic or uncontrolled:planned, and as a consequence demands that we approach its study with a different kind of intellectual apparatus (Dolphijn 2021, 15–19). With this in mind, it is an interesting exercise to reconsider the equally irregular earthwork plans of other henge enclosures such as Durrington Walls and Mount Pleasant (Fig. 14). Avebury's maverick geometry may not be so unique after all.

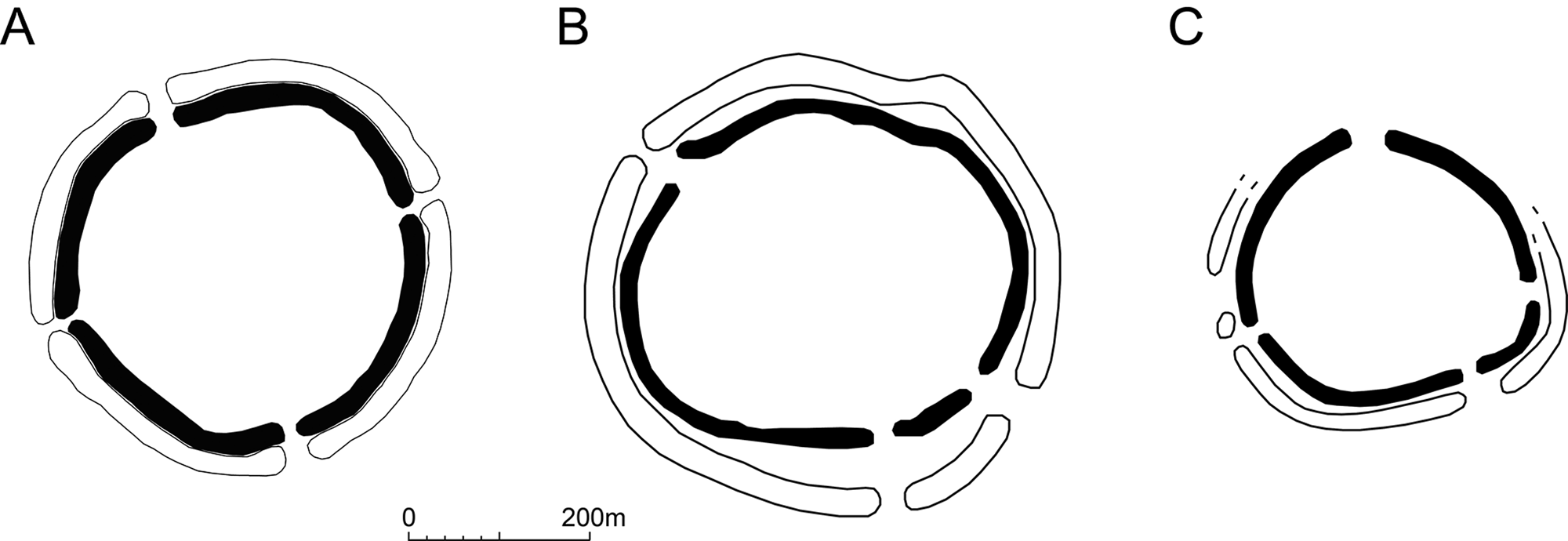
Figure 14. (A) Avebury; (B) Durrington Walls; (C) Mount Pleasant.

Conclusions: calendars, cosmograms and calculators, or time machines and crucibles?

For over a decade we have been productively debating and exploring ideas of ontology, alterity and otherness. Yet, if recent attempts to explain prehistoric monuments and monumental landscapes are anything to go by, the impact of these debates on interpretation appears to have been muted. Despite the considerable intellectual ingenuity on display in these studies, when push comes to shove, the prehistoric worlds they conjure and evoke are comfortable and familiar. They are founded on mathematical and geometric principles that are readily graspable and the assumption that their role was to know and make sense of the periodicities and behaviours of our world. This does not necessarily need to be the case, but to challenge it requires us to allow for the possibility that the monuments we survey and excavate were not simply reckoning or codifying existing worlds, but were actively engaged in the generation or evocation of new ones: worlds that may have worked in a different way to our own.

If the tendency to date has been to treat structures such as Porlock Circle and Avebury as cosmocentric, the picture that is emerging from this change of focus is instead one that is profoundly cosmogenic, bound up more in world-making (and re-making) than representation. In an attempt to create an Avebury of precision and planned order, Thom et al. revealed a circle with corners. This is a structure that does not conform to geometrical archetypes but disrupts them—neither square nor circle. It is a configuration that hints at a different kind of geometry altogether, one that stresses contradiction and ambiguity rather than idealized form. At Porlock, we have a near-perfect circle, but one that has been captured in the process of inscribing and re-inscribing itself. These are structures where a host of different ideas, concepts, imperatives and perhaps ontologies were played out, not only through the raising of standing stones and earthworks, but through careful attention to processes of folding, mirroring and hybridity. They were also very much in-motion, whether dynamically so, arrested, or some combination of the two.

Harris has recently stressed the importance of developing a nuanced, relational understanding of power in order to untangle the function (doing) of monuments. To this end, he has argued that new forms of power emerged from the affective, emergent dynamism of monuments and the new forms of community (both human and non-human) that emerged within and through these structures. Through the concept of monupower (monuments-as-power), he has stressed that monuments should be seen as world-making; rather than reflecting worldviews, they were actively involved in pushing new worlds into existence (Harris 2021, 185, 190–94). Through the examples of Porlock Circle and Avebury, we can begin to look in detail at how that generalized world-making might have played out in specific places at specific times. This is the power that resides in reflections and certain recurrent ratios and the power needed to arrest dynamic movement and to accelerate time. It is the power needed to effect (perform) a given fold and the power that flowed from the new configurations, topologies and possibilities that resulted from it.

In each case, our starting point is now different. Porlock is no longer a static stone circle, one of many, whose elements may (or may not) line up with other more primordially meaningful things. It is instead arrested motion—less a structure than an agitation; a frustration. The second we admit to this possibility, our questions change, and so do the pasts we evoke as a consequence. Why was it stopped and, perhaps more importantly, how can it be restarted? What happens when it does?

At Avebury, the nomad geometry of the square-in-circle created a machine that accelerated the passage of time, rapidly moving forwards in order to presence the past. Bradley has recently drawn attention to the way in which different early–middle Neolithic (and potentially later) monuments across the British Isles may not only have expressed different conceptions of time, but were constructed in a way that ensured that the tempo and character of their subsequent history unfurled in a predictable fashion (Bradley 2020, 2). With Avebury we can perhaps take this important argument further. Compare the recent interpretation of Stonehenge as a mechanism for marking calendrical time with that of Avebury as a time-machine. Here the passage of time was not tracked, anticipated or predicted but was instead actively manipulated: sped up and slowed down.

As with Porlock Circle, our starting point is different here too. Rather than probe Avebury in order to tease out its underlying spatial logic, we instead need to confront questions such as why it was gathering recalcitrant megaliths together; what was the significance of the repeated mirrors and reflections; why was it actively manipulating time; and what do the hybridity of its form and material vibrancy of its elements in turn conjure? Only by placing the insights gained from over a decade of debate on ontology and alterity at the front of our engagements with the data we have assembled will we be able to think ourselves away from the familiar interpretative patterns that have textured more than a century of academic research on prehistoric monumentality. As noted in the introduction, a growing body of work that seeks to do precisely this is already under way. By approaching axes not through the lens of alignment, but instead that of the fold;¹ stressing the importance of approximation and ratio instead of precision and quanta; opening up the possibility of a very different kind of geometry; and by regarding ground plans not as static representations of formal spatial logics, but instead as brimming with motion and energy, the present discussion has sought to respond to Fowles and Weismantel's calls to bring to light the otherness of the past in order to spur creative engagement. In demonstrating how well-studied and seemingly familiar monuments can quickly become very, very unfamiliar, it has hopefully created the platform and impetus for very different kinds of narrative interpretation to emerge.