Published online by Cambridge University Press: 31 May 2012
A series of samples of the twospotted spider mite, Tetranychus urticae Koch, from 16 experimental populations on “Totem” strawberry, Fragaria × ananassa Duch., were examined to determine the index of dispersion, the variance–mean relationship, the distribution, and the relationship between the mean number of T. urticae/leaflet and the proportion of leaflets without T. urticae. The slope of the variance–mean relationship, 1.64 ± 0.0355(SE), did not differ between sample dates but the intercept decreased significantly (p < 0.01) from 2.56 ± 0.0969 before harvest to 1.76 ± 0.140 during harvest. At 0.0136 T. urticae/leaflet before harvest and 0.0644 T. urticae/leaflet during harvest, the variance equaled the mean, implying that at these densities the data followed the Poisson distribution. Above these densities the data were overdispersed, most samples conforming with the negative binomial distribution but some tending towards greater dispersion than the negative binomial. There was no common k for the negative binomial nor did the data fit the expectation for 1/k that was consistent with the variance–mean relationship. A distribution-free sampling scheme based on the sample mean and the proportion of leaflets without T. urticae (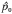 ) was developed. Tetranychus urticae density can be quickly determined in the field using the naked eye, by iteratively observing leaflets for the presence or absence of T. urticae and referring to a small table that gives both the mean density for a given
) was developed. Tetranychus urticae density can be quickly determined in the field using the naked eye, by iteratively observing leaflets for the presence or absence of T. urticae and referring to a small table that gives both the mean density for a given 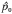 and the number of leaflets required to obtain a specified standard error.
and the number of leaflets required to obtain a specified standard error.
Une série d’échantillons du tétranyque à deux points, Tetranychus urticae Koch, prélevés de 16 populations expérimentales sur le fraisier “Totem”, Fragaria × ananassa Duch., ont été examinés pour déterminer l’indice de dispersion, la relation variance–moyenne, la distribution et le rapport entre le nombre moyen de T. urticae/foliole et la proportion de folioles sans T. urticae. La pente de la relation variance–moyenne, 1,64 ± 0,0355 (SE), ne diffère pas entre les dates d’échantillonnage, mais le point d’intersection diminue significativement, passant de 2,56 ± 0,0969 avant la récolte à 1,76 ± 0,140 pendant larécolte. À 0,0136 T. urticae/foliole avant et 0,0644 T. urticae/foliole pendant, la variance égale la moyenne, ce qui signifie qu’à ces densités, les données suivent la distribution de Poisson. Au-dessus de ces densités, les données sont très dispersées, la plupart des échantillons suivant la distribution bionomiale négative, mais certains tendant à montrer une plus grande dispersion que la binomiale négative. Il n’existe pas de coefficient k commun pour la binomiale négative et les données ne correspondent pas à la prévision d’un rapport 1/k conforme à la relation variance–moyenne. Un plan d’échantillonnage indépendant de la distribution, basé sur la moyenne des échantillons et la proportion de folioles sans T. urticae (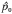 ), a été mis au point. On peut rapidement déterminer à l’oeil nu la densité du tétranyque en plein champ en observant itérativement les folioles pour la présence ou l’absence de T. urticae et en consultant une petite table qui donne la densité moyenne pour un
), a été mis au point. On peut rapidement déterminer à l’oeil nu la densité du tétranyque en plein champ en observant itérativement les folioles pour la présence ou l’absence de T. urticae et en consultant une petite table qui donne la densité moyenne pour un 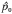 donné et le nombre de folioles nécessaires pour obtenir une erreur-type particulière.
donné et le nombre de folioles nécessaires pour obtenir une erreur-type particulière.