No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 07 November 2014
The Keynesian faith in the effectiveness of fiscal policy consists in the belief that there is a positive rate of change of national income with respect to autonomous expenditure. This in turn stems from the belief that the marginal efficiency schedule is downward-sloping. This dependence can be seen from a simple formulation of the Keynesian system. Letting Y be national income, E1 investment expenditure, E2 autonomous expenditure, r the marginal efficiency of capital, i the interest rate, and M the stock of money:
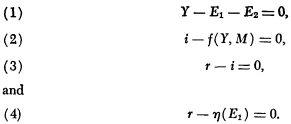
The dependent variables are Y, E1, r, and i. The derivative dY/dE2, evaluated from (1)–(4),is the expression:
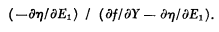
The addition of dE1/dt to the right side of (3) yields a differential-equation system whose solution is stable only if the denominator of this expression is positive. It follows that dY/dE2, the rate of change of national income with respect to autonomous expenditure, is opposite in sign to ∂η/∂E1, the slope of the marginal efficiency schedule.
This article is based on the author's MA thesis at McGill University, “The Hyper Quantity Theory of Money,” April 1956, esp. 21–8, and on a similar argument by J. A. Stock-fisch, “The Relationship between Money Cost, Investment and Rate of Return,” Quarterly Journal of Economics, May 1956. The author is grateful to Professor J. C. Weldon of McGill University for helpful comments and encouragement in the preparation of this article.
1 It may be noted that the numerator of this expression would be unaffected by the addition of an income-induced consumption component, C(Y), to the right side of (1).
2 See Keynes, J. M., General Theory of Employment, Interest and Money (London, 1936), 136.Google Scholar See also Lerner, A. P., Economics of Control (New York, 1944), chap. 25.Google Scholar
3 An assumption about the value of the marginal product of the capital good over its life in both industries is required to formulate equation f 12. The assumption that these values are constant at P 1 F 1 and P 2 F 2 is sufficient for the form of f 12 which is used.
4 See Appendix.
5 Linear homogeneity of production functions turns out to be a sufficient condition for a positive value of di/dM, evaluated from f 1–f 12, regardless of relative factor proportions (see n. 7). A positive value of di/dM has important implications for monetary policy, indicating that the Hicksian “IS” curve is upward-sloping and that an addition to the money supply produces a decrease rather than an increase in the volume of idle balances; hence “The Hyper Quantity Theory of Money.”
6 See Frazer, R. A., Duncan, W. J., and Collar, A. R., Elementary Matrices (Cambridge, 1957).Google Scholar
7 The derivative di/dM is: (∂f/∂M) A 10, 11/A, ∂f/∂M being negative. With linear homogeneous production functions, this expression becomes:
which is positive.