No CrossRef data available.
Published online by Cambridge University Press: 12 May 2020
We introduce a dimension group for a self-similar map as the 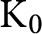 $\mathrm {K}_0$
-group of the core of the C*-algebra associated with the self-similar map together with the canonical endomorphism. The key step for the computation is an explicit description of the core as the inductive limit using their matrix representations over the coefficient algebra, which can be described explicitly by the singularity structure of branched points. We compute that the dimension group for the tent map is isomorphic to the countably generated free abelian group
$\mathrm {K}_0$
-group of the core of the C*-algebra associated with the self-similar map together with the canonical endomorphism. The key step for the computation is an explicit description of the core as the inductive limit using their matrix representations over the coefficient algebra, which can be described explicitly by the singularity structure of branched points. We compute that the dimension group for the tent map is isomorphic to the countably generated free abelian group 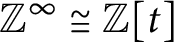 ${\mathbb Z}^{\infty }\cong {\mathbb Z}[t]$
together with the unilateral shift, i.e. the multiplication map by t as an abstract group. Thus the canonical endomorphisms on the
${\mathbb Z}^{\infty }\cong {\mathbb Z}[t]$
together with the unilateral shift, i.e. the multiplication map by t as an abstract group. Thus the canonical endomorphisms on the 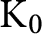 $\mathrm {K}_0$
-groups are not automorphisms in general. This is a different point compared with dimension groups for topological Markov shifts. We can count the singularity structure in the dimension groups.
$\mathrm {K}_0$
-groups are not automorphisms in general. This is a different point compared with dimension groups for topological Markov shifts. We can count the singularity structure in the dimension groups.