Article contents
On the triple correlations of fractional parts of 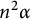 $n^2\alpha $
$n^2\alpha $
Published online by Cambridge University Press: 04 May 2021
Abstract
For fixed 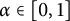 $\alpha \in [0,1]$
, consider the set
$\alpha \in [0,1]$
, consider the set 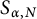 $S_{\alpha ,N}$
of dilated squares
$S_{\alpha ,N}$
of dilated squares 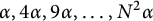 $\alpha , 4\alpha , 9\alpha , \dots , N^2\alpha \, $
modulo
$\alpha , 4\alpha , 9\alpha , \dots , N^2\alpha \, $
modulo 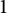 $1$
. Rudnick and Sarnak conjectured that, for Lebesgue, almost all such
$1$
. Rudnick and Sarnak conjectured that, for Lebesgue, almost all such 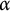 $\alpha $
the gap-distribution of
$\alpha $
the gap-distribution of 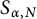 $S_{\alpha ,N}$
is consistent with the Poisson model (in the limit as N tends to infinity). In this paper, we prove a new estimate for the triple correlations associated with this problem, establishing an asymptotic expression for the third moment of the number of elements of
$S_{\alpha ,N}$
is consistent with the Poisson model (in the limit as N tends to infinity). In this paper, we prove a new estimate for the triple correlations associated with this problem, establishing an asymptotic expression for the third moment of the number of elements of 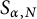 $S_{\alpha ,N}$
in a random interval of length
$S_{\alpha ,N}$
in a random interval of length 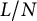 $L/N$
, provided that
$L/N$
, provided that 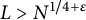 $L> N^{1/4+\varepsilon }$
. The threshold of
$L> N^{1/4+\varepsilon }$
. The threshold of 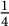 $\tfrac {1}{4}$
is substantially smaller than the threshold of
$\tfrac {1}{4}$
is substantially smaller than the threshold of 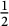 $\tfrac {1}{2}$
(which is the threshold that would be given by a naïve discrepancy estimate).
$\tfrac {1}{2}$
(which is the threshold that would be given by a naïve discrepancy estimate).
Unlike the theory of pair correlations, rather little is known about triple correlations of the dilations 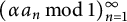 $(\alpha a_n \, \text {mod } 1)_{n=1}^{\infty } $
for a nonlacunary sequence
$(\alpha a_n \, \text {mod } 1)_{n=1}^{\infty } $
for a nonlacunary sequence 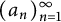 $(a_n)_{n=1}^{\infty } $
of increasing integers. This is partially due to the fact that the second moment of the triple correlation function is difficult to control, and thus standard techniques involving variance bounds are not applicable. We circumvent this impasse by using an argument inspired by works of Rudnick, Sarnak, and Zaharescu, and Heath-Brown, which connects the triple correlation function to some modular counting problems.
$(a_n)_{n=1}^{\infty } $
of increasing integers. This is partially due to the fact that the second moment of the triple correlation function is difficult to control, and thus standard techniques involving variance bounds are not applicable. We circumvent this impasse by using an argument inspired by works of Rudnick, Sarnak, and Zaharescu, and Heath-Brown, which connects the triple correlation function to some modular counting problems.
In Appendix B, we comment on the relationship between discrepancy and correlation functions, answering a question of Steinerberger.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
While the work toward this paper was being carried out, NT was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 786758) and by the Austrian Science Fund (FWF): project J-4464. A.W. is supported by a Junior Research Fellowship from Trinity College Cambridge, and was also supported by a Post-Doctoral Fellowship at the Centre de Recherches Mathématiques.
References
- 5
- Cited by



