Published online by Cambridge University Press: 20 October 2022
We derive three critical exponents for Bernoulli site percolation on the uniform infinite planar triangulation (UIPT). First, we compute explicitly the probability that the root cluster is infinite. As a consequence, we show that the off-critical exponent for site percolation on the UIPT is 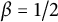 $\beta = 1/2$. Then we establish an integral formula for the generating function of the number of vertices in the root cluster. We use this formula to prove that, at criticality, the probability that the root cluster has at least n vertices decays like
$\beta = 1/2$. Then we establish an integral formula for the generating function of the number of vertices in the root cluster. We use this formula to prove that, at criticality, the probability that the root cluster has at least n vertices decays like 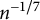 $n^{-1/7}$. Finally, we also derive an expression for the law of the perimeter of the root cluster and use it to establish that, at criticality, the probability that the perimeter of the root cluster is equal to n decays like
$n^{-1/7}$. Finally, we also derive an expression for the law of the perimeter of the root cluster and use it to establish that, at criticality, the probability that the perimeter of the root cluster is equal to n decays like 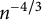 $n^{-4/3}$. Among these three exponents, only the last one was previously known. Our main tools are the so-called gasket decomposition of percolation clusters, generic properties of random Boltzmann maps, and analytic combinatorics.
$n^{-4/3}$. Among these three exponents, only the last one was previously known. Our main tools are the so-called gasket decomposition of percolation clusters, generic properties of random Boltzmann maps, and analytic combinatorics.
This work is partially supported by the ANR grant ProGraM (Projet-ANR-19-CE40-0025) and the Labex MME-DII (ANR11-LBX-0023-01).