Hostname: page-component-6bf8c574d5-r4mrb Total loading time: 0 Render date: 2025-03-07T03:16:28.723Z Has data issue: false hasContentIssue false
  • English
  • Français

Restricted sumsets in multiplicative subgroups

Part of: Sequences and sets Graph theory Additive number theory; partitions

Published online by Cambridge University Press:  09 January 2025

Chi Hoi Yip Open the ORCID record for Chi Hoi Yip [Opens in a new window]
Chi Hoi Yip*
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, United States
*
e-mail: cyip30@gatech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish the restricted sumset analog of the celebrated conjecture of Sárközy on additive decompositions of the set of nonzero squares over a finite field. More precisely, we show that if $q>13$ is an odd prime power, then the set of nonzero squares in $\mathbb {F}_q$ cannot be written as a restricted sumset 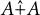$A \hat {+} A$, extending a result of Shkredov. More generally, we study restricted sumsets in multiplicative subgroups over finite fields as well as restricted sumsets in perfect powers (over integers) motivated by a question of Erdős and Moser. We also prove an analog of van Lint–MacWilliams’ conjecture for restricted sumsets, which appears to be the first analogue of Erdős--Ko–Rado theorem in a family of Cayley sum graphs.

Keywords

Restricted sumsetadditive decompositionmultiplicative subgroupSidon setCayley sum graph

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity 11P70: Inverse problems of additive number theory, including sumsets
Secondary: 11B13: Additive bases, including sumsets 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 25
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of the author was supported in part by an NSERC fellowship.

References

Alon, N., Nathanson, M. B., and Ruzsa, I. The polynomial method and restricted sums of congruence classes . J. Number Theory 56(1996), no. 2, 404–417.CrossRefGoogle Scholar
Asgarli, S. and Yip, C. H., Van Lint–MacWilliams’ conjecture and maximum cliques in Cayley graphs over finite fields . J. Combin. Theory Ser. A 192(2022), Paper No. 105667, 23.CrossRefGoogle Scholar
Bergelson, V., Kolesnik, G., Madritsch, M., Son, Y., and Tichy, R., Uniform distribution of prime powers and sets of recurrence and van der Corput sets in ${\mathbb{Z}}^k$ . Israel J. Math. 201(2014), no. 2, 729–760.CrossRefGoogle Scholar
Blokhuis, A., On subsets of with square differences . Nederl. Akad. Wetensch. Indag. Math. 46(1984), no. 4, 369–372.CrossRefGoogle Scholar
Bugeaud, Y. and Mignotte, M. , L’équation de Nagell-Ljunggren $\frac{x^n-1}{x-1}={y}^q$ . Enseign. Math. (2) 48(2002), nos. 1-2, 147–168.Google Scholar
Caporaso, L., Harris, J. , and Mazur, B., Uniformity of rational points . J. Amer. Math. Soc. 10(1997), no. 1, 1–35.CrossRefGoogle Scholar
Choudhry, A., Sextuples of integers whose sums in pairs are squares . Int. J. Number Theory. 11(2015), no. 2, 543–555.CrossRefGoogle Scholar
Dias da Silva, J. A. and Hamidoune, Y. O., Cyclic spaces for Grassmann derivatives and additive theory . Bull. London Math. Soc. 26(1994), no. 2, 140–146.CrossRefGoogle Scholar
Erdős, P., Quelques problèmes de théorie des nombres . In: Monographies de L’Enseignement Mathématique, 6, Université de Genève, L’Enseignement Mathématique, Geneva, 1963, pp 81–135.Google Scholar
Erdős, P., Ko, C., and Rado, R., Intersection theorems for systems of finite sets . Quart. J. Math. Oxford Ser. 2(1961), no. 12, 313–320.CrossRefGoogle Scholar
Gallagher, P. X., A larger sieve . Acta Arith. 18(1971), 77–81.CrossRefGoogle Scholar
Godsil, C. and Meagher, K., Erdős-Ko-Rado theorems: algebraic approaches, Cambridge Studies in Advanced Mathematics, 149 Cambridge University Press, Cambridge, 2016.Google Scholar
Green, B., Counting sets with small sumset, and the clique number of random Cayley graphs . Combinatorica 25(2005), no. 3, 307–326.CrossRefGoogle Scholar
Green, B. and Morris, R., Counting sets with small sumset and applications . Combinatorica 36(2016), no. 2 129–159.CrossRefGoogle Scholar
Gyarmati, K., On a problem of Diophantus . Acta Arith. 97(2001), no. 1, 53–65.CrossRefGoogle Scholar
Hanson, B. and Petridis, G., Refined estimates concerning sumsets contained in the roots of unity . Proc. Lond. Math. Soc. (3). 122(2021), no. 3, 353–358.CrossRefGoogle Scholar
Hindry, M. and Silverman, J. H., Diophantine geometry: An introduction, Graduate Texts in Mathematics, 201, Springer-Verlag, New York, 2000.CrossRefGoogle Scholar
Horn, R. A. and Johnson, C. R., Matrix analysis, 2nd ed., Cambridge University Press, Cambridge, 2013.Google Scholar
Lagrange, J., Six entiers dont les sommes deux à deux sont des carrés . Acta Arith. 40(1981/82), no. 1, 91–96.CrossRefGoogle Scholar
Lev, V. F. and Sonn, J., Quadratic residues and difference sets . Q. J. Math. 68(2017), no. 1, 79–95.Google Scholar
Lidl, R. and Niederreiter, H., Finite fields, 2nd ed., Encyclopedia of Mathematics and Its Applications, 20, Cambridge University Press, Cambridge, 1997, With a foreword by P. M. Cohn.Google Scholar
Nagell, T., Des équations indéterminées ${x}^2+x+1={y}^n$ et ${x}^2+x+1=3{y}^n$ , Norsk Mat. Forenings Skr, 2(1920).Google Scholar
Nicolas, J.-L., $6$ nombres dont les sommes deux à deux sont des carrés. Bull. Soc. Math. France Mém. 49–50(1977), 141–143.CrossRefGoogle Scholar
Rivat, J., Sárközy, A., and Stewart, C. L.. Congruence properties of the $\varOmega$ -function on sumsets . Illinois J. Math. 43(1999), no. 1, 1–18.CrossRefGoogle Scholar
Sárközy, A., On additive decompositions of the set of quadratic residues modulo $p$ . Acta Arith. 155(2012), no. 1, 41–51.CrossRefGoogle Scholar
Shkredov, I. and Solymosi, J., The uniformity conjecture in additive combinatorics . SIAM J. Discrete Math. 35(2021), no. 1, 307–321.CrossRefGoogle Scholar
Shkredov, I. D., Sumsets in quadratic residues . Acta Arith. 164(2014), no. 3, 221–243.CrossRefGoogle Scholar
Shkredov, I. D., Difference sets are not multiplicatively closed . Discrete Anal., 17(2016), 21.Google Scholar
Shkredov, I. D., Any small multiplicative subgroup is not a sumset . Finite Fields Appl. 63(2020), 101645, 15.CrossRefGoogle Scholar
Shparlinski, I. E., Additive decompositions of subgroups of finite fields . SIAM J. Discrete Math. 27(2013), no. 4, 1870–1879.CrossRefGoogle Scholar
Sierpiński, W., A selection of problems in the theory of numbers, The Macmillan Company, New York, 1964. Translated from the Polish by A. Sharma.Google Scholar
Stepanov, S. A., On the number of points of a hyperelliptic curve over a finite prime field . Izv. Akad. Nauk SSSR, Ser. Mat. 33(1969),1171–1181.Google Scholar
Sziklai, P., On subsets of with $d$ th power differences. Discrete Math. 208(1999), no. 209, 547–555.Google Scholar
van Lint, J. H. and MacWilliams, F. J., Generalized quadratic residue codes . IEEE Trans. Inform. Theory. 24(1978), no. 6, 730–737.CrossRefGoogle Scholar
Yip, C. H., On the directions determined by Cartesian products and the clique number of generalized Paley graphs . Integers 21(2021). Paper No. A51, 31.Google Scholar
Yip, C. H., Gauss sums and the maximum cliques in generalized Paley graphs of square order . Funct. Approx. Comment. Math. 66(2022), no. 1, 119–138.CrossRefGoogle Scholar
Yip, C. H., Additive decompositions of large multiplicative subgroups in finite fields . Acta Arith. 213(2024), no. 2, 97–116.CrossRefGoogle Scholar