Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T04:48:54.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Adic Topologies for the Rational Integers

Published online by Cambridge University Press:  20 November 2018

Kevin A. Broughan
Kevin A. Broughan*
Affiliation:
University of Waikato, Hamilton, New Zealand e-mail: kab@waikato.ac.nz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

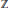A topology on $\mathbb{Z}$, which gives a nice proof that the set of prime integers is infinite, is characterised and examined. It is found to be homeomorphic to 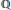$\mathbb{Q}$, with a compact completion homeomorphic to the Cantor set. It has a natural place in a family of topologies on 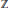$\mathbb{Z}$, which includes the 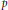$p$-adics, and one in which the set of rational primes $\mathbb{P}$ is dense. Examples from number theory are given, including the primes and squares, Fermat numbers, Fibonacci numbers and $k$-free numbers.

Keywords

11B0511B2511B5013J1013B35p-adic, metrizablequasi-valuationtopological ringcompletioninverse limitdiophantine equationprime integersFermat numbersFibonacci numbers
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 4 , 01 August 2003 , pp. 711 - 723
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Apostol, T. M., Introduction to Analytic Number Theory. New York, Berlin, Heidelberg, Springer-Verlag, 1976.Google Scholar
[2] Aigner, M. and Ziegler, G. M., Proofs from the Book. Springer-Verlag, 1998.Google Scholar
[3] Engelking, R., Outline of General Topology. North-Holland, 1968.Google Scholar
[4] Kaplansky, I., Topological Rings. Amer. J. Math. 69(1947), 153–183.Google Scholar
[5] Mahler, K., P-adic numbers and their functions. Cambridge, Cambridge University Press, 1981 Google Scholar
[6] Morris, S. A., Pontryagin Duality and the structure of locally compact abelian groups. London Math. Soc. Lecture Notes in Math. 29, Cambridge, 1977.Google Scholar
[7] Ribenboim, P., The New Book of Prime Number Records. Springer-Verlag, 1999.Google Scholar
[8] Schoenfeld, A. H. and Gruenhage, G., An alternate characterization of the Cantor set. Proc. Amer. Math. Soc. 53(1975), 235–236.Google Scholar
[9] Sierpinski, W., Sur une propriété topologique des ensembles dénombrables denses en soi. Fund. Math. 1(1920), 11–16.Google Scholar