Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T20:06:41.191Z Has data issue: false hasContentIssue false
  • English
  • Français

Admissibility for a Class of Quasiregular Representations

Published online by Cambridge University Press:  18 June 2019

Bradley N. Currey
Bradley N. Currey*
Affiliation:
Department of Mathematics and Computer Science, Saint Louis University, Saint Louis, MO 63103, U.S.A. email: curreybn@slu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a semidirect product 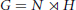$G\,=\,N\,\rtimes \,H$ where 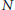$N$ is nilpotent, connected, simply connected and normal in 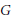$G$ and where 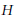$H$ is a vector group for which 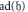$ad(\mathfrak{h})$ is completely reducible and 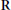$\mathbf{R}$-split, let 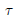$\tau $ denote the quasiregular representation of 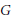$G$ in 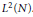${{L}^{2}}(N)$. An element 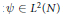$\psi \,\in \,{{L}^{2}}(N)$ is said to be admissible if the wavelet transform 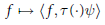$f\,\mapsto \,\left\langle f,\,\tau (\cdot )\psi \right\rangle $ defines an isometry from 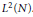${{L}^{2}}(N)$ into 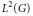${{L}^{2}}(G)$. In this paper we give an explicit construction of admissible vectors in the case where 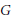$G$ is not unimodular and the stabilizers in 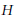$H$ of its action on 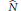$\hat{N}$ are almost everywhere trivial. In this situation we prove orthogonality relations and we construct an explicit decomposition of 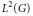${{L}^{2}}(G)$ into 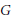$G$-invariant, multiplicity-free subspaces each of which is the image of a wavelet transform . We also show that, with the assumption of (almost-everywhere) trivial stabilizers, non-unimodularity is necessary for the existence of admissible vectors.

Keywords

22E2722E30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 5 , 01 October 2007 , pp. 917 - 942
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Arnal, D.,BenAmmar, M., Currey, B., and Dali, B., Explicit construction of canonical coordinates for completely solvable Lie groups. J. Lie Theory 15(2005), 521–560.Google Scholar
[2] Currey, B., A continuous trace composition sequence for C*(G) where G is an exponential solvable Lie group . Math. Nachr. 159(1992), 189–212.Google Scholar
[3] Currey, B., An explicit Plancherel formula for completely solvable Lie groups. MichiganMath. J. 38(1991), no. 1, 75–87.Google Scholar
[4] Currey, B., Explicit orbital parameters and the Plancherel measure for exponential Lie groups. Pacific J. Math. (to appear).Google Scholar
[5] Currey, B., Smooth decomposition of finite multiplicity monomial representations for a class of completely solvable homogeneous spaces. Pacific J. Math. 170(1995), no. 2, 429–460.Google Scholar
[6] Currey, B., The structure of the space of coadjoint orbits of an exponential solvable Lie group. Trans. Amer. Math. Soc. 332(1992), no. 1, 241–269.Google Scholar
[7] Currey, B. and Penney, R., The structure of the space of co-adjoint orbits of a completely solvable Lie group. Mich. Math. J. 36(1989), no. 2, 309–320.Google Scholar
[8] Duflo, M. and Moore, C., On the regular representation of a nonunimodular locally compact group. J. Functional Analysis 21(1976), no. 2, 209–243.Google Scholar
[9] Duflo, M. and Raïs, M., Sur l’analyse harmonique sur les groupes de Lie résolubles. Ann. Sci. École Norm. Sup. 9(1976), no. 1, 107–144.Google Scholar
[10] Fabec, R., and Ólafsson, G., The continuous wavelet transform and symmetric spaces. Acta Applicandae Math. (to appear)Google Scholar
[11] Führ, H., Admissible vectors for the regular representation. Proc. Amer. Math. Soc. 130(2002), no. 10, 2959–2970.(electronic).Google Scholar
[12] Ishi, H., Wavelet transforms for semidirect product groups. J. Fourier Anal. Appl. 12(2006), no. 1, 37–52.Google Scholar
[13] Laugesen, R. S., Weaver, N., Weiss, G., and Wilson, E. N., A characterization of the higher dimensional groups associated with continuous wavelets. J. Geom. Anal. 12(2002), no. 1, 89–102.Google Scholar
[14] Lipsman, R., Harmonic analysis on exponential solvable homogeneous spaces: the algebraic or symmetric cases. Pacific. J. Math. 140(1989), no. 1, 117–147.Google Scholar
[15] Lipsman, R., Induced representations of completely solvable Lie groups. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 17(1990), no. 1, 127–164.Google Scholar
[16] Lipsman, R., The multiplicity function on exponential and completely solvable homogeneous spaces. Geom. Dedicata 39(1991), no. 2, 155–161.Google Scholar
[17] Lipsman, R. and Wolf, J., Canonical semi-invariants and the Plancherel formula for parabolic groups. Trans. Amer. Math. Soc. 269(1982), no. 1, 111–131.Google Scholar
[18] Liu, H. and Peng, L., Admissible wavelets associated with the Heisenberg group. Pacific J. Math. 180(1997), no. 1, 101–123.Google Scholar
[19] Pedersen, N. V., On the infinitesimal kernel of irreducible representations of nilpotent Lie groups. Bull. Soc. Math. France 112(1984), no. 4, 423–467.Google Scholar
[20] Pukánszky, L., On the characters and the Plancherel formula of nilpotent Lie groups. J. Functional Analysis 1(1967), 255–280.Google Scholar
[21] Pukánszky, L., On the unitary representations of exponential Lie groups. J. Functional Analysis 2(1968), 73–113.Google Scholar
[22] Weiss, G. and Wilson, E. N., The mathematial theory of wavelets. In: Twentieth Century Harmonic Analysis – A Celebration, NATO Sci. Ser. II Math. Phys. Chem. 33, Kluwer Acad. Publ., Dordrecht, 2001, pp. 329–366.Google Scholar