Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T17:57:14.915Z Has data issue: false hasContentIssue false
  • English
  • Français

Affine Lines on Affine Surfaces and the Makar–Limanov Invariant

Published online by Cambridge University Press:  20 November 2018

R. V. Gurjar ,
K. Masuda ,
M. Miyanishi  and
P. Russell
R. V. Gurjar
Affiliation:
School of Mathematics, Tata Institute for Fundamental Research, Homi Bhabha Road, Mumbai 400005, India e-mail: gurjar@math.tifr.res.in
K. Masuda
Affiliation:
Graduate School of Material Sciences, University of Hyogo, Himeji 671-2201, Japan e-mail: kayo@sci.u-hyogo.ac.jp
M. Miyanishi
Affiliation:
School of Science and Technology, Kwansei Gakuin University, Hyogo 669-1337, Japan e-mail: miyanisi@ksc.kwansei.ac.jp
P. Russell
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, QC, H3A 2K6 e-mail: russell@math.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

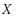A smooth affine surface $X$ defined over the complex field 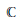$\mathbb{C}$ is an 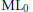$\text{M}{{\text{L}}_{0}}$ surface if the Makar–Limanov invariant 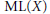$\text{ML(}X\text{)}$ is trivial. In this paper we study the topology and geometry of 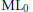$\text{M}{{\text{L}}_{0}}$ surfaces. Of particular interest is the question: Is every curve 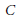$C$ in 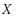$X$ which is isomorphic to the affine line a fiber component of an 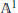${{\mathbb{A}}^{1}}$-fibration on 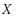$X$? We shall show that the answer is affirmative if the Picard number 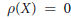$\rho (X)\,=\,0$, but negative in case 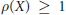$\rho (X)\,\ge \,1$. We shall also study the ascent and descent of the 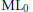$\text{M}{{\text{L}}_{0}}$ property under proper maps.

Keywords

Primary14R20secondary14L30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 1 , 01 February 2008 , pp. 109 - 139
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Andreotti, A. and Siu, Y. T., Projective embedding of pseudoconcave spaces. Ann. Scuola. Norm. Sup. Pisa 24(1970), 231–278.Google Scholar
[2] Andreotti, A. and Tomassini, G., Some remarks on pseudoconcave manifolds. In: Essays on Topology and Related Topics. Springer-Verlag, New York, 1970, pp. 85–104.Google Scholar
[3] Cassou-Noguès, P. and Russell, P., Birational endomorphisms C2 → C2 and affine ruled surfaces. In: Affine Algebraic Geometry. Osaka University Press, Osaka, 2007, pp. 57–105.Google Scholar
[4] Daigle, D. and Russell, P., Affine rulings of normal rational surfaces. Osaka J. Math. 38(2001), no. 1, 37–100.Google Scholar
[5] Daigle, D. and Russell, P., On log Q-homology planes and weighted projective planes Canad. J. Math. 56(2004), no. 3, 1145–1189.Google Scholar
[6] Derksen, H., Constructive Invariant Theory and the Linearisation Problem. Ph.D. thesis, University of Basel, 1997.Google Scholar
[7] Fujita, T., On the topology of noncomplete algebraic surfaces. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 29(1982), no. 3, 503–566.Google Scholar
[8] Gizatullin, M. H., Affine surfaces that can be augmented by a nonsingular rational curve. Izv. Akad. Nauk SSSR Ser. Mat. 34(1970), 778–802.Google Scholar
[9] Gizatullin, M. H., Quasihomogeneous affine surfaces. Izv. Akad. Nauk SSSR Ser.Mat. 35(1971), 1047–1071.Google Scholar
[10] Gurjar, R. V., A new proof of Suzuki's formula. Proc. Indian Acad. Sci. (Math. Sci.) 107(1997), no. 3, 237–242.Google Scholar
[11] Gurjar, R. V. and Miyanishi, M., On contractible curves in the complex affine plane. Tohoku Math. J. 48(1996), no. 3, 459–469.Google Scholar
[12] Gurjar, R. V. and Miyanishi, M., Affine lines on logarithmic Q-homology planes. Math. Ann. 294 (1992), no. 3, 463–482.Google Scholar
[13] Gurjar, R. V. and Miyanishi, M., Automorphisms of affine surfaces with A1-fibrations. MichiganMath. J. 53(2005), no. 1, 33–55.Google Scholar
[14] Gurjar, R. V. and Shastri, A. R., The fundamental group at infinity of affine surfaces. Comment.Math. Helv. 59 (1984), no. 3, 459–484.Google Scholar
[15] Iitaka, S., Algebraic Geometry. An Introduction to Birational Geometry of Algebraic Varieties. Graduate Texts in Mathematics 76, Springer-Verlag, New York, 1982.Google Scholar
[16] Kobayashi, R., Uniformization of complex surfaces. Kähler metric and moduli spaces. Adv. Stud. Pure Math. 18-II, Academic Press, Boston, MA, 1990, pp. 313–394.Google Scholar
[17] Masuda, K. and Miyanishi, M., The additive group actions on Q-homology planes. Ann. Inst. Fourier (Grenoble) 53(2003), no. 2, 429–64.Google Scholar
[18] Miyanishi, M., Curves on rational and unirational surfaces. Tata Institute of Fundamental Research Lectures on Mathematics and Physics 60. Narosa Publishing House, New Delhi, 1978.Google Scholar
[19] Miyanishi, M., Noncomplete algebraic surfaces. Lecture Notes in Mathematics 857, Springer-Verlag, Berlin, 1981.Google Scholar
[20] Miyanishi, M., Open Algebraic Surfaces. CRM Monograph Series 12, American Mathematical Society, Providence, RI, 2001.Google Scholar
[21] Miyanishi, M., Regular subrings of a polynomial ring. Osaka J. Math. 17(1980), no. 2, 329–338.Google Scholar
[22] Miyanishi, M., Normal affine subalgebras of a polynomial ring. In: Algebraic and Topological Theories. Kinokuniya, Tokyo, 1985, pp. 37–51.Google Scholar
[23] Miyanishi, M. and Sugie, T., Homology planes with quotient singularities. J. Math. Kyoto Univ. 31(1991), no. 3, 755–788.Google Scholar
[24] Nori, M. V., Zariski's conjecture and related problems. Ann. Sci. École Norm. Sup. 16(1983), 305–344.Google Scholar
[25] Ramanujam, C. P., A topological characterisation of the affine plane as an algebraic variety. Ann. of Math. 94(1971), 69–88.Google Scholar
[26] Sumihiro, H., Equivariant completion. J. Math. Kyoto Univ. 14(1974), 1–28.Google Scholar
[27] Sumihiro, H., Equivariant completion. II. J. Math. Kyoto Univ. 15(1975), 573–605.Google Scholar
[28] Suzuki, M., Sur les opérations holomorphes du groupe additif sur l’espace de deux variables complexes. Ann. Sci. École Norm. Sup. 10(1977), no. 4, 517–546.Google Scholar
[29] Yoshihara, H., On plane rational curves. Proc. Japan Acad. Ser. A Math. Sci. 55(1979), 152–551.Google Scholar
[30] Zaidenberg, M., Isotrivial families of curves on affine surfaces and the characterizations of the affine plane. Math. USSR. Izv. 30(1988), no. 3, 503–532.Google Scholar
[31] Zaidenberg, M. G. and Orevkov, S. Y., On rigid rational cuspidal plane curves. Russian Math. Surveys. 51(1996), no. 1, 179–180.Google Scholar