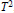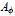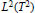Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Seto, Michio
2004.
On the Berger-Coburn-Lebow Problem for Hardy Submodules.
Canadian Mathematical Bulletin,
Vol. 47,
Issue. 3,
p.
456.
Seto, Michio
2004.
Invariant Subspaces on 𝕋Nand ℝN.
Canadian Mathematical Bulletin,
Vol. 47,
Issue. 1,
p.
100.
SETO, Michio
2005.
Submodules of $L^2(\mathbf{R}^2)$.
Tokyo Journal of Mathematics,
Vol. 28,
Issue. 2,