No CrossRef data available.
Article contents
Almost-Free E-Rings of Cardinality ℵ1
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
An 
$E$-ring is a unital ring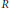 
$R$ such that every endomorphism of the underlying abelian group 
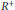${{R}^{+}}$ is multiplication by some ring element. The existence of almost-free $E$-rings of cardinality greater than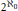 
${{2}^{{{\aleph }_{0}}}}$ is undecidable in ZFC. While they exist in Gödel's universe, they do not exist in other models of set theory. For a regular cardinal 
${{\aleph }_{1}}\le \text{ }\!\!\lambda\!\!\text{ }\le {{2}^{{{\aleph }_{0}}}}$ we construct $E$-rings of cardinality 
$\lambda $ in ZFC which have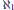 
${{\aleph }_{1}}$-free additive structure. For 
$\text{ }\!\!\lambda\!\!\text{ }={{\aleph }_{1}}$ we therefore obtain the existence of almost-free $E$-rings of cardinality 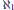${{\aleph }_{1}}$ in ZFC.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2003
References
[1] Bowshell, R. and Schultz, P., Unital rings whose additive endomorphisms commute. Math. Ann.
228(1977), 197–214.Google Scholar
[2] Casacuberta, C., Rodríguez, J. and Tai, J., Localizations of abelian Eilenberg-Mac-Lane spaces of finite type. Prepublications, Universitat Autònoma de Barcelona 22(1997).Google Scholar
[3] Corner, A. L. S. and Göbel, R., Prescribing endomorphism algebras. Proc. London Math. Soc. (3)
50(1985), 447–479.Google Scholar
[5] Dugas, M. and Göbel, R., Torsion-free nilpotent groups and E-modules. Arch. Math. (4)
45(1990), 340–351.Google Scholar
[6] Dugas, M., Mader, A. and Vinsonhaler, C., Large E-rings exist. J. Algebra (1)
108(1987), 88–101.Google Scholar
[7] Eklof, P. and Mekler, A., Almost free modules, Set-theoretic methods.
North-Holland, Amsterdam, 1990.Google Scholar
[8] Faticoni, T., Each countable reduced torsion-free commutative ring is a pure subring of an E-ring. Comm. Algebra (12)
15(1987), 2545–2564.Google Scholar
[9] Feigelstock, S., Additive Groups Of Rings Vol. I. Pitman Advanced Publishing Program, Boston, London, Melbourne, 1983.Google Scholar
[10] Feigelstock, S., Additive Groups Of Rings Vol. II. Pitman Research Notes in Math. Series 169(1988).Google Scholar
[11] Fuchs, L., Infinite Abelian Groups.Volume I.
Academic Press, New York, London, 1970.Google Scholar
[12] Fuchs, L., Infinite Abelian Groups.Volume II.
Academic Press, New York, London, 1973.Google Scholar
[14] Göbel, R. and Shelah, S., Indecomposable almost free modules.the local case. Canad. J. Math.
50(1998), 719–738.Google Scholar
[15] Göbel, R. and Shelah, S., On the existence of rigid ℵ1
-free abelian groups of cardinality ℵ1
. In: Abelian Groups and Modules, Proceedings of the Padova Conference, 1994, 227–237.Google Scholar
[16] Göbel, R. and Strüngmann, L., Almost-free E(R)-algebras and E(A, R)-modules. Fund. Math.
169(2001), 175–192.Google Scholar
[17] Niedzwecki, G. and Reid, J., Abelian groups cyclic and projective as modules over their endomorphism rings. J. Algebra
159(1993), 139–149.Google Scholar
[18] Pierce, R. S. and Vinsonhaler, C., Classifying E-rings. Comm. Algebra
19(1991), 615–653.Google Scholar
[19] Reid, J., Abelian groups finitely generated over their endomorphism rings. Springer Lecture Notes in Math. 874, 1981, 41–52.Google Scholar
[20] Schultz, P., The endomorphism ring of the additive group of a ring. J. Austral. Math. Soc.
15(1973), 60–69.Google Scholar
You have
Access