Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T21:31:57.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Amenability and Covariant Injectivity of Locally Compact Quantum Groups II

Published online by Cambridge University Press:  20 November 2018

Jason Crann
Jason Crann*
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON, Canada KlS 5B6 e-mail: jason.crann@carleton.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

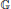Building on our previous work, we study the non-relative homology of quantum group convolution algebras. Our main result establishes the equivalence of amenability of a locally compact quantum group $\mathbb{G}$ and 1-injectivity of 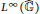${{L}^{\infty }}\left( \widehat{\mathbb{G}} \right)$ as an operator 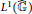${{L}^{1}}\left( \widehat{\mathbb{G}} \right)$-module. In particular, a locally compact group 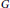$G$ is amenable if and only if its group von Neumann algebra 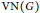$\text{VN}\left( G \right)$ is 1-injective as an operator module over the Fourier algebra 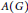$A\left( G \right)$. As an application, we provide a decomposability result for completely bounded 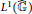${{L}^{1}}\left( \widehat{\mathbb{G}} \right)$-module maps on 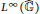${{L}^{\infty }}\left( \widehat{\mathbb{G}} \right)$, and give a simplified proof that amenable discrete quantum groups have co-amenable compact duals, which avoids the use of modular theory and the Powers-Størmer inequality, suggesting that our homological techniques may yield a new approach to the open problem of duality between amenability and co-amenability.

Keywords

22D3546M1046L89locally compact quantum groupamenabilityinjective module
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 5 , 01 October 2017 , pp. 1064 - 1086
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Bédos, E. and Tuset, L., Amenability and co-amenability for locally compact quantum groups. Internat. J. Math. 14(2003), no. 8, 865–884. http://dx.doi.Org/10.1142/S01291 67X03002046 Google Scholar
[2] Blecher, D. P., The standard dual of an operator space. Pacific J. Math. 153(1992), no. 1,15–30.http://dx.doi.Org/10.2140/pjm.1992.1 53.15 Google Scholar
[3] Blecher, D. P. and Le Merdy, C., Operator algebras and their modules: an operator space approach. London Mathematical Society Monographs, New Series, 30. Clarendon Press, Oxford, 2004.Google Scholar
[4] Choi, M.-D. and Effros, E. G., Nuclear C* -algebras and injectivity: the general case. Indiana Univ. Math. J. 26(1977), no. 3, 443–446.http://dx.doi.Org/10.1512/iumj.1977.26.26034 Google Scholar
[5] Connes, A., Classification of injective factors. Cases . Ann. of Math. (2) 104(1976), no. 1, 73–115.http://dx.doi.Org/10.2307/1971057 Google Scholar
[6] Crann, J., On hereditary properties of quantum group amenability. Proc. Amer. Math. Soc. 145(2017), no. 2, 627–635.http://dx.doi.Org/10.1090/proc/13365 Google Scholar
[7] Crann, J. and Neufang, M., Amenability and covariant injectivity of locally compact quantum groups. Trans. Amer. Math. Soc. 368(2016), 495–513.http://dx.doi.Org/10.1090/tran/6374 Google Scholar
[8] Crann, J. and Tanko, Z., On the operator homology of the Fourier algebra and its cb-multiplier completion. arxiv:1602.05259 Google Scholar
[9] Dales, H. G. and Polyakov, M. E., Homological properties of modules over group algebras. Proc. London Math. Soc. (3) 89(2004), no. 2, 390–426. http://dx.doi.org/10.112/S0024611504014686 Google Scholar
[10] Daws, M., Multipliers, self-induced and dual Banach algebras. Dissertationes Math. 470(2010). http://dx.doi.org/10.4064/dm470-0-1 Google Scholar
[11] Daws, M., Completely positive multipliers of quantum groups. Internat. J. Math. 23(2012), no. 12, 1250132.http://dx.doi.Org/10.1142/S0129167X12501327 Google Scholar
[12] de Canniére, J., and Haagerup, U., Multipliers of the Fourier algebras of some simple Lie groups and their discrete subgroups. Amer. J. Math. 107(1985), no. 2, 455–500.http://dx.doi.org/10.2307/2374423 Google Scholar
[13] Desmedt, P., Quaegebeur, J., and Vaes, S., Amenability and the bicrossed product construction. Illinois J. Math. 46(2002), no. 4,1259–1277.Google Scholar
[14] Effros, E. G. and Lance, C. E., Tensor products of operator algebras. Adv. Math. 25(1977), no. 1,1–34.HTTP://DX.DOI.ORG/10.1016/0001-8708(77)90085-8 Google Scholar
[15] Effros, E. G. and Ruan, Z.-J., Operator spaces. London Mathematical Society Monographs, New Series, 23. Oxford University Press, New York, 2000.Google Scholar
[16] Guichardet, A., Tensor products of C* -algebras. Aarhus University Lecture Notes Series no. 12, 1969.Google Scholar
[17] Haagerup, U., Injectivity and decomposition of completely bounded maps. In: Operator algebras and their connections with topology and ergodic theory (Busteni, 1983). Lecture Notes in Math., 1132. Springer, Berlin, 1985, pp. 170–222.http://dx.doi.Org/10.1OO7/BFbOO74885 Google Scholar
[18] Haagerup, U. and J.|Kraus, Approximation properties for group C* -algebras and group von Neumann algebras. Trans. Amer. Math. Soc. 44(1994), no. 2, 667–699. http://dx.doi.Org/10.2307/2154501 Google Scholar
[19] Helemskii, A. Y., Metric version of flatness andHahn-Banach type theorems for normed modules over sequence algebras. Studia Math. 206(2011), no. 2,135–160.http://dx.doi.org/10.4064/sm206-2-3 Google Scholar
[20] Hu, Z., Neufang, M., and Ruan, Z.-J., Multipliers on a new class of Banach algebras, locally compact quantum groups, and topological centres. Proc. Lond. Math. Soc. (3) 100(2010), no. 2, 429–458.http://dx.doi.Org/10.1112/plms/pdpO26 Google Scholar
[21] Hu, Z., Completely bounded multipliers over locally compact quantum groups. Proc. Lond. Math. Soc. (3) 103(2011), no. 1, 1–39.http://dx.doi.Org/10.1112/plms/pdqO41 Google Scholar
[22] Hu, Z., Convolution of trace class operators over locally compact quantum groups. Canad. J. Math. 65(2013), no. 5, 1043–1072.http://dx.doi.org/10.4153/CJM-2012-030-5 Google Scholar
[23] Junge, M., Neufang, M., and Ruan, Z.-J., A representation theorem for locally compact quantum groups. Internat. J. Math. 20(2009), no. 3, 377–400.http://dx.doi.Org/10.1142/S01291 67X09005285 Google Scholar
[24] Kalantar, M., Compact operators in regular LCQ groups. Canad. Math. Bull. 57(2014), no. 3, 546–550.http://dx.doi.org/10.4153/CMB-2013-003-5 Google Scholar
[25] Kalantar, M. and Neufang, M., Duality, cohomology, and geometry of locally compact quantum groups. J. Math. Anal. Appl. 406(2013), no. 1, 22–33.http://dx.doi.Org/10.1016/j.jmaa.2O13.04.024 Google Scholar
[26] Kraus, J., J and Ruan, Z.-J., Approximation properties for Kac algebras. Indiana Univ. Math. J. 48(1999), no. 2, 469–535.http://dx.doi.org/10.1512/iumj.1999.48.1660 Google Scholar
[27] Kustermans, J., Locally compact quantum groups in the universal setting. Internat. J. Math. 12(2001), no. 3, 289–338.http://dx.doi.Org/1 0.1142/S0129167X01000757 Google Scholar
[28] Kustermans, J. and Vaes, S., Locally compact quantum groups in the von Neumann algebraic setting. Math. Scand. 92(2003), no. 1, 68–92.Google Scholar
[29] Lance, C. E., On nuclear C* -algebras. J. Funct. Anal. 12(1973), 157–176.Google Scholar
[30] Leptin, H., Sur l'algé bre de Fourier d'un groupe localement compact. C. R. Acad. Sci. Paris Sér. A-B 266(1968), A1180–A1182.Google Scholar
[31] Neufang, M., Ruan, Z.-J. and Spronk, N., Completely isometric representations of Mcb,A(G) and . Trans. Amer. Math. Soc. 360(2008), no. 3,1133–1161.http://dx.doi.org/10.1090/S0002-9947-07-03940-2 Google Scholar
[32] Paulsen, V. I., Every completely polynomially bounded operator is similar to a contraction. J. Funct. Anal. 55(1984), no. 1, 1–17.http://dx.doi.Org/1 0.1016/0022-1236(84)90014-4 Google Scholar
[33] Pisier, G., Introduction to operator space theory. London Mathematical Society Lecture Note Series, 294. Cambridge University Press, Cambridge, 2003.http://dx.doi.Org/10.1017/CBO97811 07360235 Google Scholar
[34] Renaud, P. F., Invariant means on a class of von Neumann algebras. Trans. Amer. Math. Soc. 170(1972),285–291.http://dx.doi.org/10.1090/S0002-9947-1972-0304553-0 Google Scholar
[35] Ruan, Z.-J., Amenability of Hopf von Neumann algebras and Kac algebras. J. Funct. Anal. 139(1996), no. 2, 466–499. http://dx.doi.Org/10.1006/jfan.1 996.0093 Google Scholar
[36] Soltan, P. and Viselter, A., A note on amenability of locally compact quantum groups. Canad. Math. Bull. 57(2014), no. 2, 424–430.http://dx.doi.org/10.4153/CMB-2O12-032-3 Google Scholar
[37] Takesaki, M., A characterization of group algebras as a converse of Tannaka-Stinespring-Tatsuuma duality theorem. Amer. J. Math. 91(1969), 529–564.http://dx.doi.Org/10.2307/2373525 Google Scholar
[38] Takesaki, M., Theory of operator algebras II. Encyclopedia of Mathematical Sciences, 125. Springer-Verlag, Berlin, 2003. http://dx.doi.org/10.1007/978-3-662-10451-4 Google Scholar
[39] Takesaki, M., Theory of operator algebras III. Encyclopedia of Mathematical Sciences, 127. Springer-Verlag, Berlin, 2003.http://dx.doi.org/10.1007/978-3-662-10453-8 Google Scholar
[40] Tomatsu, R., Amenable discrete quantum groups. J. Math. Soc. Japan 58(2006), no. 4, 949–964.http://dx.doi.org/10.2969/jmsj71179759531 Google Scholar
[41] Vaes, S., Locally compact quantum groups. Ph.D. thesis, K.U. Leuven, 2000.Google Scholar
[42] Vaes, S., The unitary implementation of a locally compact quantum group action. J. Funct. Anal. 180(2001), no. 2, 426–480.http://dx.doi.Org/10.1006/jfan.2000.3704 Google Scholar
[43] Vaes, S. and Vainerman, L., On low-dimensional locally compact quantum groups. In: Locally compact quantum groups and groupoids (Strasbourg, 2002). IRMA Lect. Math. Theor. Phys., 2. de Gruyter, Berlin, 2003, pp. 127–187.Google Scholar
[44] Van Daele, A., Locally compact quantum groups. A von Neumann algebra approach. SIGMA Symmetry Integrability Geom. Methods Appl. 10(2014), 082.http://dx.doi.Org/10.3842/SICMA.2014.082 Google Scholar
[45] Woronowicz, S. L., Compact quantum groups. In: Symétries quantiques (Les Houches, 1995). North-Holland, Amsterdam, 1998, pp. 845–884.Google Scholar