Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T22:40:56.311Z Has data issue: false hasContentIssue false
  • English
  • Français

An AF Algebra Associated with the Farey Tessellation

Published online by Cambridge University Press:  20 November 2018

Florin P. Boca
Florin P. Boca*
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL 61801, U.S.A. Institute of Mathematics “Simion Stoilow” of the Romanian Academy, P.O. Box 1-764, RO-014700 Bucharest, Romania e-mail:fboca@math.uiuc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

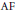We associate with the Farey tessellation of the upper half-plane an $\text{AF}$ algebra 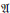$\mathfrak{A}$ encoding the “cutting sequences” that define vertical geodesics. The Effros–Shen 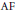$\text{AF}$ algebras arise as quotients of 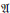$\mathfrak{A}$. Using the path algebra model for 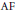$\text{AF}$ algebras we construct, for each 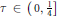$\tau \,\,\in \,\,\left( 0 \right.,\left. \frac{1}{4} \right]$, projections 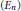$({{E}_{n}})$ in 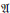$\mathfrak{A}$ such that 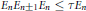${{E}_{n}}{{E}_{n\pm 1}}E\le \tau {{E}_{n}}$.

Keywords

46L0511A5511B5746L5537E0582B20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 5 , October 2008 , pp. 975 - 1000
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Bratteli, O., Inductive limits of finite dimensional C*-algebras . Trans. Amer. Math. Soc. 171(1972), 195–234.Google Scholar
[2] Bratteli, O., Structure spaces of approximately finite-dimensional C*-algebras. I. J. Funct. Anal. 16 (1974), 192–204.Google Scholar
[3] Bratteli, O., The center of approximately finite-dimensional C*-algebras. J. Funct. Anal. 21(1976), no. 2, 195–202.Google Scholar
[4] Bratteli, O. and Elliott, G. A., Structure spaces of approximately finite-dimensional C*-algebras. II. J. Funct. Anal. 30(1978), no. 1, 74–82.Google Scholar
[5] Brocot, A., Calcul des rouages par approximation. Revue Chronométrique 3(1861), 186–194.Google Scholar
[6] Carlitz, L., A problem in partitions related to Stirling numbers. Riv.Mat. Univ. Parma 5(1964), 61–75.Google Scholar
[7] Denjoy, A., Sur une fonction réelle de Minkowski. J. Math. Pures Appl. 17(1938), 105–151.Google Scholar
[8] Dixmier, J., Les C*-alg`ebres et leurs représentations. Cahiers Scientifiques 19, Gauthier-Villars, Paris, 1964.Google Scholar
[9] Dooley, A. H., The spectral theory of posets and its applications to C*-algebras. Trans. Amer. Math. Soc. 224(1976), 143–155.Google Scholar
[10] Effros, E. G., Dimensions and C*-algebras. CBMS Regional Conference Series in Mathematics 46, Conference Board of the Mathematical Sciences,Washington, D.C., 1981.Google Scholar
[11] Effros, E. G. and C.-L. Shen, Approximately finite C*-algebras and continued fractions. Indiana Univ. Math. J. 29(1980), no. 2, 191–204.Google Scholar
[12] Elliott, G. A., On the classification of inductive limits of sequences of semisimple finite-dimensional algebras. J. Algebra 38(1976), no. 1, 29–44.Google Scholar
[13] Evans, D. E. and Kawahigashi, Y., Quantum Symmetries on Operator Algebras. Oxford University Press, 1998.Google Scholar
[14] Feigenbaum, M. J., Presentation functions, fixed points and a theory of scaling function dynamics. J. Statist. Phys. 52(1988), no. 3-4, 527–569.Google Scholar
[15] Goodman, F., de la Harpe, P., and Jones, V. F. R., Coxeter Graphs and Towers of Algebras. Mathematical Sciences Research Institute Publications 14, Springer–Verlag, New York, 1989.Google Scholar
[16] Fiala, J. and Kleban, P., Generalized number theoretic spin chain-connections to dynamical systems and expectation values. J. Stat. Phys. 121(2005), no. 3-4, 553–577.Google Scholar
[17] Knauf, A., On a ferromagnetic spin chain. Comm. Math. Phys. 153(1993), no. 1, 77–115.Google Scholar
[18] Knauf, A., The number-theoretical spin chain and the Riemann zeroes. Comm. Math. Phys. 196(1998), no. 3, 703–731.Google Scholar
[19] Knauf, A., Number theory, dynamical systems and statistical mechanics. Rev. Math. Phys. 11(1999), no. 8, 1027–1060.Google Scholar
[20] Minkowski, H., Gesammelte Abhandlungen. Vol. 2, B. G. Teubner, Leipzig und Berlin, 1911, pp. 50–51.Google Scholar
[21] Pimsner, M. and Voiculescu, D., Imbedding the irrational rotation C*-algebra into an AF-algebra. J. Operator Theory 4(1980), no. 2, 201–210.Google Scholar
[22] Prellberg, T., Fiala, J., and Kleban, P., Cluster approximation for the Farey fraction spin chain. J. Statist. Phys. 123(2006), no. 2, 455–471.Google Scholar
[23] Raeburn, I. and Williams, D. P., Morita Equivalence and Continuous-Trace C*-Algebras. Mathematical Surveys and Monographs 60, American Mathematical Society, Providence, RI, 1998.Google Scholar
[24] Salem, R., On some singular monotonic functions which are strictly increasing. Trans. Amer. Math. Soc. 53(1943), 427–439.Google Scholar
[25] Series, C., The modular surface and continued fractions. J. London Math. Soc. 31(1985), no. 1, 69–80.Google Scholar
[26] Sloane, N., Encyclopedia of Integer Sequences. http://www.research.att.com/˜ njas/sequences.Google Scholar
[27] Stern, M., Über eine zahlentheoretische Funktion. J. Reine Angew. Mathematik 55(1858), 193–220.Google Scholar