Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T17:14:48.840Z Has data issue: false hasContentIssue false
  • English
  • Français

An Explicit Manin-Dem’janenko Theorem in Elliptic Curves

Published online by Cambridge University Press:  20 November 2018

Evelina Viada
Evelina Viada*
Affiliation:
Mathematisches Institut, Georg-August-Universitä, Bunsenstraße 3-5, D-D-37073, Göttingen, Germany, e-mail: evelina.viada@mathematik.uni-goettingen.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $c$ be a curve of genus at least 2 embedded in 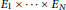${{E}_{1}}\,\times \,.\,.\,.\,\times \,{{E}_{N}}$ , where the 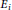${{\text{E}}_{i}}$ are elliptic curves for 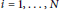$i\,=\,1,\,.\,.\,.\,,\,N$. In this article we give an explicit sharp bound for the Néron–Tate height of the points of $c$ contained in the union of all algebraic subgroups of dimension 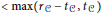$<\,\max ({{r}_{C}}\,-{{t}_{C}},\,{{t}_{C}})$ , where 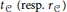${{t}_{C}}(\text{resp}\text{.}{{r}_{C}})$ is the minimal dimension of a translate (resp. of a torsion variety) containing $c$.

As a corollary, we give an explicit bound for the height of the rational points of special curves, proving new cases of the explicit Mordell Conjecture and in particular making explicit (and slightly more general in the CM case) the Manin–Dem’janenko method for curves in products of elliptic curves.

Keywords

11G5014G40heightelliptic curveexplicit Mordell conjectureexplicit Manin-Demjanenko theoremrational points on a curve
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 5 , 01 October 2018 , pp. 1173 - 1200
Copyright
Copyright © Canadian Mathematical Society 2018

References

[BG06] Bombieri, E. and Gubler, W., Heights in Diophantine geometry. New Mathematical Monographs, 4, Cambridge University Press, Cambridge, 2006.Google Scholar
[BMZ99] Bombieri, E., Masser, D., and Zannier, U., Intersecting a curve with algebraic subgroups of multiplicative groups. Internat. Math. Res. Notices 20 (1999), 1119–1140.Google Scholar
[BV83] Bombieri, E. and Vaaler, J., On Siegel's lemma. Invent. Math. 73 (1983) no. 1,11-32. http://dx.doi.org/10.1007/BF01393823Google Scholar
[BGS94] Bost, J.-B., Gillet, H., and Soulé, C., Heights of protective varieties and positive Green forms. J. Amer. Math. Soc. 7 (1994), no. 4, 903–1027. http://dx.doi.Org/10.1090/S0894-0347-1 994-1260106-XGoogle Scholar
[Cha41] Chabauty, C., Sur les points rationnels des courbes algébriques de genre supérieur à l'unité. C. R. Acad. Sci. Paris 212 (1941), 882–885.Google Scholar
[CVV17] Checcoli, S., Veneziano, F., and Viada, E., On the explicit torsion anomalous conjecture. Trans. Amer. Math. Soc. 369 (2017), 6465–6491. http://dx.doi.Org/10.1090/tran/6893Google Scholar
[CVV16] Checcoli, S., Veneziano, F., and Viada, E., The explicit Mordell conjecture for families of curves. 2016. arxiv:1602.04097Google Scholar
[CV14] Checcoli, S. and Viada, E., On the torsion anomalous conjecture in CM abelian varieties. Pacific J. Math. 271 (2014), no. 2, 321–345. http://dx.doi.org/10.2140/pjm.2014.271.321Google Scholar
[Col85] Coleman, R. F., Effective Chabauty. Duke Math. J. 52 (1985), 765–780. http://dx.doi.org/10.1215/S0012-7094-85-05240-8Google Scholar
[Cox89] Cox, D. A., Primes of the form x2 + ny2. Wiley, New York, 1989.Google Scholar
[Dem68] Dem'janenko, V., Rational points on a class of algebraic curves, Amer. Math. Soc. Transi. 66 (1968), 246–272.Google Scholar
[HabO8] Habegger, P., Intersecting subvarieties ofGn m with algebraic subgroups. Math. Ann. 342 (2008), no. 2, 449–466. http://dx.doi.Org/10.1007/s00208-008-0242-3Google Scholar
[Fal83] Faltings, G., Endlichkeitssàtze fur abelsche Varietàten iiber Zahlkb'rpern. Invent. Math. 73 (1983), 349–366. http://dx.doi.org/10.1007/BF01388432Google Scholar
[Kul99] Kulesz, L., Application de la méthode de Dem'janenko-Manin à certaines familles de courbes de genre 2 et 3. J. Number Theory 76 (1999) no. 1, 130–146.Google Scholar
[KMS04] Kulesz, L., Matera, G., and Schost, E., Uniform bounds for the number of rational points of families of curves of genus 2. J. Number Theory 108, (2004), 241–267.Google Scholar
[Man69] Manin, J., The p-torsion of elliptic curves is uniformly bounded. Isv. Akad. Nauk. SSSR Ser. Mat. 33 (1969), 459–465. http://dx.doi.Org/10.1006/jnth.1998.2339Google Scholar
[MP10] McCallum, W. and Poonen, B., The method of Chabauty and Coleman. In: Explicit methods in number theory; rational points and diophantine equations, Panoramas et Synthèses, 36, Soc. Math. France, Paris, 2012, pp. 99-117.Google Scholar
[MW90] Masser, D. and Wiistholz, G., Estimating isogenies on elliptic curves. Invent. Math. 100 (1990), 1–24.Google Scholar
[MW93] Masser, D. and Wiistholz, G., Periods and minimal abelian subvarieties. Ann. of Math. (2) 137 (1993), no. 2, 407–458. http://dx.doi.org/10.2307/2946542Google Scholar
[Neu99] Neukirch, J., Algebraic number theory. Grundlehren der Mathematischen Wissenschaften, Springer-Verlag, Berlin, 1999.Google Scholar
[Phi91] Philippon, P., Sur des hauteurs alternatives. I. Math. Ann. 289 (1991), no. 2, 255–284. http://dx.doi.org/10.1007/BF01446571Google Scholar
[Phi95] Philippon, P., Sur des hauteurs alternatives. III. J. Math. Pures Appl. (9) 74 (1995), no. 4, 345–365.Google Scholar
[Phil2] Philippon, P., Sur une question d'orthogonalité dans les puissances de courbes elliptiques. 2012. https://hal.archives-ouvertes.fr/hal-00801376/documentGoogle Scholar
[Ser89] Serre, J.-P., Lectures on the Mordell-Weil theorem. Aspects of Mathematics, E15, Friedr. Vieweg & Sohn, Braunschweig, 1989.Google Scholar
[Sil86] Silverman, J. H., The arithmetic of elliptic curves. Graduate Texts in Mathematics, 106, Springer-Verlag, New York, 1986.Google Scholar
[Sil90] Silverman, J. H., The difference between the Weil height and the canonical height on elliptic curves. Math. Comp. 55 (1990), no. 192, 723–743. http://dx.doi.org/10.1090/S0025-5718-1990-1035944-5Google Scholar
[Stoll] Stoll, M., Rational points on curves. J. Théor. Nombres Bordeaux 23 (2011), 257–277. http://dx.doi.org/10.5802/jtnb.760Google Scholar
[ViaO3] Viada, E., The intersection of a curve with algebraic subgroups in a product of elliptic curves. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 2 (2003), no. 1, 47–75.Google Scholar
[ViaO8] Viada, E., The intersection of a curve with a union of translated codimension-two subgroups in a power of an elliptic curve. Algebra Number Theory 2 (2008), no. 3, 249–298. http://dx.doi.Org/10.2140/ant.2008.2.249Google Scholar
[Vial5] Viada, E., Explicit height bounds and the effective Mordell-Lang Conjecture. Riv. Math. Univ. Parma (N.S.) 7 (2016) no. 1,101-131.Google Scholar
[Winl7] Winckler, B.. Problème de Lehmer sur les courbes elliptiques à multiplications complexes. 2017. https://hal.archives-ouvertes.fr/hal-01 493577Google Scholar
[Zanl2] Zannier, U., Some problems of unlikely intersections in arithmetic and geometry (with appendixes by D. Masser). Annals of Mathematics Studies, 181, Princeton University Press, Princeton, NJ, 2012.Google Scholar
[Zha95] Zhang, S., Positive line bundles on arithmetic varieties. J. Amer. Math. Soc. 8 (1995), no. 1, 187–221. http://dx.doi.org/10.1090/S0894-0347-1995-1254133-7Google Scholar