Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T13:55:52.308Z Has data issue: false hasContentIssue false
  • English
  • Français

An Explicit Polynomial Expression for a q-Analogue of the 9- j Symbols

Published online by Cambridge University Press:  20 November 2018

Mizan Rahman
Mizan Rahman*
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON email: mrahman@math.carleton.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using standard transformation and summation formulas for basic hypergeometric series we obtain an explicit polynomial form of the $q$-analogue of the 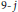$\text{9-}\,j$ symbols, introduced by the author in a recent publication. We also consider a limiting case in which the 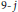$\text{9-}\,j$ symbol factors into two Hahn polynomials. The same factorization occurs in another limit case of the corresponding $q$-analogue.

Keywords

33D4533D506-j and 9-j symbolsq-analoguesbalanced and very-well-poised basic hypergeometric seriesorthonormal polynomials in one and two variablesRacah and q-Racah polynomials and their extensions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 1 , 01 February 2011 , pp. 200 - 221
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Ališauskas, S., The triple sum formulas for 9 j coefficients of SU(2) and uq(2). J. Math. Phys. 41 (2000), no. 11, 7589-7610. doi:10.1063/1.1312198Google Scholar
[2] Ališauskas, S., The multiple sum formulas for 9- j and 12- j coefficients of SU(2) and uq(2). arXiv:math/9912142v5.Google Scholar
[3] Alişauskas, S. and A. P., Jucys, Weight lowering operators and the multiplicity-free isoscalar factors for the group R5. J. Mathematical Phys. 12 (1971), 594-605. doi:10.1063/1.1665626Google Scholar
[4] Aomoto, K. and, Kita, M., Theory of hypergeometric functions. (Japanese), Springer, Tokyo, 1994.Google Scholar
[5] Askey, R. and, J. A., Wilson, A set of polynomials that generalize Racah coefficients or 6- j symbols. SIAM J. Math. Anal. 10 (1979), no. 5, 1008-1016. doi:10.1137/0510092Google Scholar
[6] Askey, R. and, Wilson, J. A., Some basic hypergeometric orthogonal polynomials that generalize Jacobi polynomials. Mem. Amer. Math. Soc. 54 (1985), no. 319.Google Scholar
[7] Bailey, W. N., Generalized hypergeometric series. Cambridge Tracts in Mathematics and Mathematical Physics, 32, Stechert-Hafner, Inc., New York, 1964.Google Scholar
[8] Edmonds, A. R., Angular momentum in quantum mechanics. In: Investigations in Physics, Vol. 4, Princeton University Press, Princeton, NJ, 1957.Google Scholar
[9] Erdèlyi, A., Higher Transcendental Functions. Bateman Manuscript Project, McGraw-Hill, New York, 1953.Google Scholar
[10] Gasper, G. and, Rahman, M., Basic hypergeometric series. Second ed., Encyclopedia of Mathematics and its Applications, 96, Cambridge University Press, Cambridge, 2004.Google Scholar
[11] Hoare, M. and, Rahman, M., A probabilistic origin for a new class of bivariate polynomials. SIGMA Symmetry Integrability Geom. Methods Appl. 4 (2008), Paper 089.Google Scholar
[12] Hoare, M. and, Rahman, M., Cumulative Bernoulli trials and Krawtchouk processes. Stochastic Process. Appl. 16 (1984), no. 2, 113-139. doi:10.1016/0304-4149(84)90014-0Google Scholar
[13] Ismail, M. E. H., Classical and quantum orthogonal polynomials in one variable. Encyclopedia of Mathematics and its Applications, 98, Cambridge University Press, Cambridge, 2005.Google Scholar
[14] Kirillov, A. N. and Yu Reshetikhin, N., Representations of the algebraUq(s(2)), q-orthogonal polynomials and invariants of links. In: Infinite-dimensional Lie algebras and groups (Luminy-Marseille, 1988), Adv. Ser. Math. Phys., 7, World Sci. Publ. Teaneck, NJ, 1989.Google Scholar
[15] Landau, L. D. and Lifschitz, E. M., Quantum mechanics: non-relativistic theory. Second ed., Addison-Wesley, Reading, MA, 1965.Google Scholar
[16] Mizukawa, H., Zonal spherical functions on the complex reflection groups and (n + 1,m + 1)-hypergeometric functions. Adv. Math. 184 (2004), 1-17. doi:10.1016/S0001-8708(03)00092-6Google Scholar
[17] Nomura, M., Various kinds of relation for 3n- j symbols of quantum group SUq(2). J. Phys. Soc. Japan 59 (1990), no. 11, 3851-3860. doi:10.1143/JPSJ.59.3851Google Scholar
[18] Racah, G., Theory of complex spectra. II. Phys. Rev. 62 (1942), 438-462.Google Scholar
[19] Rahman, M., A q-analogue of the 9- j symbols and their orthogonality. J. Approx. Theory 161 (2009), no. 1, 239-258. doi:10.1016/j.jat.2008.09.008Google Scholar
[20] Rosengren, H., Another proof of the triple sum formula for Wigner 9 j-symbols. J. Math. Phys. 40 (1999), no. 12, 6689-6691. doi:10.1063/1.533114Google Scholar
[21] Suslov, S. K., The 9 j-symbols as orthogonal polynomials in two discrete variables. (Russian) Yadernaya Fiz. 38 (1983), no. 4, 1102-1104.Google Scholar
[22] On the theory of 9 j-symbols. (Russian) Teoret. Mat. Fiz. 88 (1991), no. 1, 66-71.Google Scholar
[23] Wilson, J. A., Hypergeometric, recurrence relations and some new orthogonal polynomials, Ph. D. Thesis, University of Wisconsin, Madison, 1978.Google Scholar
[24] Wilson, J. A., Some hypergeometric orthogonal polynomials. SIAM J. Math. Anal. 11 (1980), no. 4, 690-701. doi:10.1137/0511064Google Scholar
[25] Zhedanov, A., j-symbols of the oscillator algebra and Krawtchouk polynomials in two variables. J. Phys. A 30 (1997), 8337-8353. doi:10.1088/0305-4470/30/23/029Google Scholar