Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-16T00:57:02.539Z Has data issue: false hasContentIssue false
  • English
  • Français

An Extension of the Concept of the Order Dual of a Riesz Space

Published online by Cambridge University Press:  20 November 2018

W. A. J. Luxemburg  and
J. J. Masterson
W. A. J. Luxemburg
Affiliation:
California Institute of Technology and Michigan State University
J. J. Masterson
Affiliation:
California Institute of Technology and Michigan State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

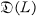Let L be a σ-Dedekind complete Riesz space. In (8), H. Nakano uses an extension of the multiplication operator on a Riesz space into itself (analagous to the closed operator on a Hilbert space) to obtain a representation space for the Riesz space L. He calls such an operator a “dilatator operator on L.” More specifically, he shows that the set of all dilatator operators , when suitable operations are defined, is a Dedekind complete Riesz space which is isomorphic to the space of all functions defined and continuous on an open dense subset of some fixed totally disconnected Hausdorff space. The embedding of L in the function space is then obtained by showing that L is isomorphic to a Riesz subspace of 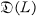. Moreover, when L is Dedekind complete, it is an ideal in 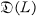, and the topological space is extremally disconnected.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 488 - 498
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Kaplan, S., The second dual of the space of continuous functions II, Trans. Amer. Math. Soc., 93 (1959), 329–350.Google Scholar
2. Kaplan, S., The second dual of the space of continuous functions III, Trans. Amer. Math. Soc., 101 (1961), 34–51.Google Scholar
3. Kaplan, S., The second dual of the space of continuous functions IV, Trans. Amer. Math. Soc., 113 (1964), 512–546.Google Scholar
4. Luxemburg, W. A. J. and Zaanen, A. C., Notes on Banach functions spaces VIII, Nederl. Akad. Wetensch. Proc Ser. A, 67, 1 (1964), 104–119.Google Scholar
5. Luxemburg, W. A. J. and Zaanen, A. C., Notes on Banach functions spaces IX, Nederl. Akad. Wetensch. Proc. Ser. A, 6, 1 (1964), 360–376.Google Scholar
6. Luxemburg, W. A. J. and Zaanen, A. C., Notes on Banach functions spaces X, Nederl. Akad. Wetensch. Proc. Ser. A, 67, 1 (1964), 493–506.Google Scholar
7. Luxemburg, W. A. J. and Zaanen, A. C., Notes on Banach functions spaces XVI, Nederl. Akad. Wetensch. Proc. Ser. A, 68, 1 (1965), 646–667.Google Scholar
8. Nakano, H., Modern spectral theory (Tokyo, 1950).Google Scholar