Article contents
Analytic Properties of Power Product Expansions
Published online by Cambridge University Press: 20 November 2018
Abstract
Let ƒ(z) be a complex function analytic in some neighbourhood of the origin with ƒ(0) = 1. It is known that ƒ(z) admits a unique "power product" expansion of the form 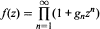 convergent near zero. We derive a simple direct bound for the radius of convergence of this product expansion in terms of the coefficients of ƒ(z). In addition we show that the same bound holds in the case of "inverse power product" expansions
convergent near zero. We derive a simple direct bound for the radius of convergence of this product expansion in terms of the coefficients of ƒ(z). In addition we show that the same bound holds in the case of "inverse power product" expansions 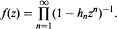 Examples are given for which these bounds are sharp. We show also that products with nonnegative coefficients have the same radius of convergence as their corresponding series.
Examples are given for which these bounds are sharp. We show also that products with nonnegative coefficients have the same radius of convergence as their corresponding series.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1995
References
- 7
- Cited by


