Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T03:21:42.268Z Has data issue: false hasContentIssue false
  • English
  • Français

Annihilators for the Class Group of a Cyclic Field of Prime Power Degree, II

Published online by Cambridge University Press:  20 November 2018

Cornelius Greither  and
Radan Kučera
Cornelius Greither
Affiliation:
Institut für theoretische Informatik und Mathematik, Fakultät für Informatik, Universität der Bundeswehr München, 85579 Neubiberg, Germany e-mail: cornelius.greither@unibw.de
Radan Kučera
Affiliation:
Přírodovědecká fakulta, Masarykova univerzita, Janáčkovo nám. 2a, 60200 Brno, Czech Republic e-mail: kucera@math.muni.cz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove, for a field 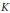$K$ which is cyclic of odd prime power degree over the rationals, that the annihilator of the quotient of the units of 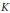$K$ by a suitable large subgroup (constructed from circular units) annihilates what we call the non-genus part of the class group. This leads to stronger annihilation results for the whole class group than a routine application of the Rubin–Thaine method would produce, since the part of the class group determined by genus theory has an obvious large annihilator which is not detected by that method; this is our reason for concentrating on the non-genus part. The present work builds on and strengthens previous work of the authors; the proofs are more conceptual now, and we are also able to construct an example which demonstrates that our results cannot be easily sharpened further.

Keywords

11R3311R2011Y40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 3 , 01 June 2006 , pp. 580 - 599
Copyright
Copyright © Canadian Mathematical Society 2006

References

[BH] Burns, D. and Hayward, A., Explicit units and the Equivariant Tamagawa number conjecture. II. Preprint: http://www.mth.kcl.uk/staff/dj_burns/gk3/ps Google Scholar
[F] Fröhlich, A., Central Extensions, Galois Groups, and Ideal Class Groups of Number Fields. Contemporary Mathematics 24, American Mathematical Society, Providence, RI, 1983.Google Scholar
[GK1] Greither, C. and Kučcera, R., The lifted root number conjecture for fields of prime degree over the rationals: an approach via trees and Euler systems. Ann. Inst. Fourier (Grenoble) 52(2002), 735–777.Google Scholar
[GK2] Greither, C. and Kučcera, R., Annihilators for the class group of a cyclic field of prime power degree. Acta Arith. 112(2004), no. 2, 177–198.Google Scholar
[H] Hayward, A., A class number formula for higher derivatives of abelian L-functions. Compositio Math. 140(2004), no. 1, 99–129.Google Scholar
[Ka1] Kaplansky, I., Commutative Rings. Polygonal Publishing House, Washington, NJ, 1994.Google Scholar
[Ka2] Kaplansky, I., Fields and Rings. Second ed. Chicago Lectures in Mathematics, University of Chicago Press, Chicago 1972.Google Scholar
[RW] Ritter, J. and Weiss, A., The lifted root number conjecture for some cyclic extensions of ℚ. Acta Arith. 90(1999), no. 4, 313–340.Google Scholar
[S] Sinnott, W., On the Stickelberger ideal and the circular units of an abelian field. Invent. Math. 62(1980/81), no. 2, 181–234.Google Scholar