Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T01:29:12.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximating Flats by Periodic Flats in CAT(0) Square Complexes

Published online by Cambridge University Press:  20 November 2018

Daniel T. Wise
Daniel T. Wise*
Affiliation:
Deptartment of Mathematics and Statistics, McGill University, 805 Sherbrooke Street West, Montreal, QC, H3A 2K6, e-mail: wise@math.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the problem of whether every immersed flat plane in a nonpositively curved square complex is the limit of periodic flat planes. Using a branched cover, we reduce the problem to the case of 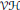$\mathcal{V}\mathcal{H}$-complexes. We solve the problem for malnormal and cyclonormal 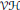$\mathcal{V}\mathcal{H}$-complexes. We also solve the problem for complete square complexes using a different approach. We give an application towards deciding whether the elements of fundamental groups of the spaces we study have commuting powers. We note a connection between the flat approximation problem and subgroup separability.

Keywords

20F6720F06CAT(0)periodic flat planes
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 2 , 01 April 2005 , pp. 416 - 448
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Berger, R., The undecidability of the domino problem. Mem. Amer. Math. Soc. 66(1966).Google Scholar
[2] Bestvina, M. and Feighn, M., Stable actions of groups on real trees. Invent.Math. 121(1995), 287–321.Google Scholar
[3] Brady, N., Branched coverings of cubical complexes and subgroups of hyperbolic groups. J. London Math. Soc. 60(1999), 461–480.Google Scholar
[4] Bridson, M. R. and Haefliger, A.,Metric spaces of non-positive curvature. GrundlehrenMath.Wiss. 319, Springer-Verlag, Berlin, 1999.Google Scholar
[5] Burns, R. G., Karrass, A., and Solitar, D., A note on groups with separable finitely generated subgroups. Bull. Austral. Math. Soc. 36(1987), 153–160.Google Scholar
[6] Buyalo, S. V., Euclidean planes in three-dimensional manifolds of nonpositive curvature.Mat. Zametki 43(1988), 103–114, 155.Google Scholar
[7] Eberlein, P., Geodesic flow in certain manifolds without conjugate points. Trans. Amer. Math. Soc. 167(1972), 151–170.Google Scholar
[8] Gromoll, D. and Wolf, J. A., Some relations between the metric structure and the algebraic structure of the fundamental group in manifolds of nonpositive curvature. Bull. Amer.Math. Soc. 77(1971), 545–552.Google Scholar
[9] Gromov, M., Hyperbolic groups. In: Essays in group theory,Math. Sci. Res. Inst. Publ. 8, Springer, New York, 1987, pp. 75–263.Google Scholar
[10] Gromov, M., Asymptotic invariants of infinite groups. In: Geometric group theory,Mathematical Society Lecture Note Series 182, Cambridge Univ. Press, Cambridge, 1993.Google Scholar
[11] Grünbaum, B. and Shephard, G. C., Tilings and patterns. Freeman, W. H., New York, 1987.Google Scholar
[12] Hsu, T. and Wise, D. T., Separating quasiconvex subgroups of right-angled Artin groups. Math. Z. 240(2002), 521–548.Google Scholar
[13] Kapovich, M., Flats in 3-manifolds. Preprint, 1998.Google Scholar
[14] Lawson, H. B., Jr. and Yau, S. T., Compact manifolds of nonpositive curvature. J. Differential Geom. 7(1972), 211–228.Google Scholar
[15] Mosher, L., Geometry of cubulated 3-manifolds. Topology 34(1995), 789–814.Google Scholar
[16] Rips, E., Subgroups of small cancellation groups. Bull. LondonMath. Soc. 14(1982), 45–47.Google Scholar
[17] Schroeder, V., Codimension one tori in manifolds of nonpositive curvature. Geom. Dedicata 33(1990), 251–263.Google Scholar
[18] Scott, P. and Wall, T., Topological methods in group theory. In: Homological group theory, London Math. Soc. Lecture Note Ser. 36, Cambridge Univ. Press, Cambridge, 1979, pp. 137–203.Google Scholar
[19] Stallings, J. R., Topology of finite graphs. Invent.Math. 71(1983), 551–565.Google Scholar
[20] Weinbaum, C. M., The word and conjugacy problems for the knot group of any tame, prime, alternating knot. Proc. Amer.Math. Soc. 30(1971), 22–26.K, 1971.Google Scholar
[21] Wise, D. T., Complete squared complexes. Preprint 2003.Google Scholar
[22] Wise, D. T., Cubulating small-cancellation groups. Geom. Funct. Anal. 14(2004), 150–214.Google Scholar
[23] Wise, D. T., Subgroup separability of the figure 8 knot group. Preprint 1998.Google Scholar
[24] Wise, D. T., Non-positively curved squared complexes, aperiodic tilings, and non-residually finite groups. PhD thesis, Princeton University, 1996.Google Scholar
[25] Wise, D. T., Subgroup separability of graphs of free groups with cyclic edge groups. Q. J. Math. 51(2000), 107–129.Google Scholar
[26] Wise, D. T., The residual finiteness of negatively curved polygons of finite groups. Invent.Math. 149(2002), 579–617.Google Scholar
[27] Wise, D. T., A flat plane that is not the limit of periodic flat planes. Algebr. Geom. Topol. 3(2003), 147–154 (electronic).Google Scholar