Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T20:19:59.363Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation on Closed Sets by Analytic or Meromorphic Solutions of Elliptic Equations and Applications

Published online by Cambridge University Press:  20 November 2018

André Boivin ,
Paul M. Gauthier  and
Petr V. Paramonov
André Boivin
Affiliation:
Department of Mathematics, University of Western Ontario, London, Ontario, N6A 5B7, e-mail: boivin@uwo.ca
Paul M. Gauthier
Affiliation:
Département de mathématiques, et de statistique, Université de Montréal, CP 6128, Succ. Centre-ville Montréal, Québec, H3C 3J7, e-mail: gauthier@dms.umontreal.ca
Petr V. Paramonov
Affiliation:
Mechanics and Mathematics Faculty, Moscow State (Lomonosov) University, 119899 Moscow, Russia, e-mail: petr@paramonov.msk.ru
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a homogeneous elliptic partial differential operator $L$ with constant complex coefficients and a class of functions (jet-distributions) which are defined on a (relatively) closed subset of a domain 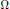$\Omega$ in 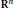${{\mathbf{R}}^{n}}$ and which belong locally to a Banach space $V$, we consider the problem of approximating in the norm of $V$ the functions in this class by “analytic” and “meromorphic” solutions of the equation 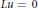$Lu\,=\,0$. We establish new Roth, Arakelyan (including tangential) and Carleman type theorems for a large class of Banach spaces $V$ and operators $L$. Important applications to boundary value problems of solutions of homogeneous elliptic partial differential equations are obtained, including the solution of a generalized Dirichlet problem.

Keywords

30D4030E1031B3535Jxx35J6741A30approximation on closed setselliptic operatorstrongly elliptic operatorL-meromorphic and L-analytic functionslocalization operatorBanach space of distributionsDirichlet problem
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 5 , 01 October 2002 , pp. 945 - 969
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Agmon, S., Lectures on Elliptic Boundary Value Problems. D. Van Nostrand, Princeton, Toronto, New York, London, 1965.Google Scholar
[2] Boivin, A. and Paramonov, P. V., Approximation by meromorphic and entire solutions of elliptic equations in Banach spaces of distributions. Mat. Sb. (4) 189 (1998), 481–502.Google Scholar
[3] Dufresnoy, A., Gauthier, P. M. and Ow, W. H., Uniform approximation on closed sets by solutions of elliptic partial differential equations. Complex Variables. 6 (1986), 235–247.Google Scholar
[4] Fuglede, B., Asymptotic paths for subharmonic functions. Math. Ann. 213 (1975), 261–274.Google Scholar
[5] Gaier, D., Lectures on Complex Approximation. Birkhäuser, Boston, Basel, Stuttgart, 1987.Google Scholar
[6] Gardiner, S. J., Harmonic Approximation. LondonMath. Society Lecture Notes 221, Cambridge University Press, 1995.Google Scholar
[7] Hörmander, L., The Analysis of Linear Partial Differential Operators I. Springer-Verlag, Berlin, New York, 1983.Google Scholar
[8] Mattila, P., Geometry of Sets and Measures in Euclidean Spaces, Cambridge University Press, 1995.Google Scholar
[9] Narasimhan, R., Analysis on Real and Complex Manifolds. North-Holland, Amsterdam, New York, Oxford, 1968.Google Scholar
[10] O'Farrell, A. G., T-invariance. Proc. Roy. Irish Acad. (2) 92A(1992), 185–203.Google Scholar
[11] Paramonov, P. V. and Verdera, J., Approximation by solutions of elliptic equations on closed subsets of Euclidean space. Math. Scand. 74 (1994), 249–259.Google Scholar
[12] Rudin, W., Real and Complex Analysis. Third Edition, McGraw Hill, New York & als, 1987.Google Scholar
[13] Sinclair, A., A general solution for a class of approximation problems. Pacific J. Math. 8 (1958), 857–866.Google Scholar
[14] Stein, E. M., Singular Integrals and Differentiability Properties of Functions. Princeton Univ. Press, Princeton, New Jersey, 1970.Google Scholar
[15] Verdera, J., Cm approximation by solutions of elliptic equations, and Calderón-Zygmund operators. Duke Math. J. 55 (1987), 157–187.Google Scholar