Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-27T11:02:06.047Z Has data issue: false hasContentIssue false
  • English
  • Français

Archimedean Closures in Lattice-Ordered Groups

Published online by Cambridge University Press:  20 November 2018

Richard D. Byrd
Richard D. Byrd*
Affiliation:
University of Houston, Houston, Texas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Conrad (10) and Wolfenstein (15; 16) have introduced the notion of an archimedean extension (a-extension) of a lattice-ordered group (l-group). In this note the class 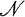of l-groups that possess a plenary subset of regular subgroups which are normal in the convex l-subgroups that cover them are studied. It is shown in § 3 (Corollary 3.4) that the class 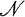is closed with respect to a-extensions and (Corollary 3.7) that each member of the class 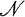has an a-closure. This extends (6, p. 324, Corollary II; 10, Theorems 3.2 and 4.2; 15, Theorem 1) and gives a partial answer to (10, p. 159, Question 1). The key to proving both of these results is Theorem 3.3, which asserts that if a regular subgroup is normal in the convex l-subgroup that covers it, then this property is preserved by a-extensions.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1004 - 1012
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Birkhoff, G., Lattice theory, rev. éd., Amer. Math. Soc. Colloq. Publ., Vol. 25 (Amer. Math. Soc, Providence, R.I., 1948).Google Scholar
2. Byrd, R. D., Lattice-ordered groups, Dissertation, Tulane University, New Orleans, Louisiana, 1966.Google Scholar
3. Byrd, R. D., Complete distributivity in lattice-ordered groups, Pacific J. Math. 20 (1967), 423–432.Google Scholar
4. Byrd, R. D. and Lloyd, J. T., Closed subgroups and complete distributivity in lattice-ordered groups, Math. Z. 101 (1967), 123–130.Google Scholar
5. Choe, T. H., The interval topology of a lattice-ordered group, Kyungpook Math. J. 2 (1959), 69–74.Google Scholar
6. Conrad, P., On ordered division rings, Proc. Amer. Math. Soc. 5 (1954), 323–328.Google Scholar
7. Conrad, P., Right-ordered groups, Michigan Math. J. 6 (1959), 267–275.Google Scholar
8. Conrad, P., Some structure theorems for lattice-ordered groups, Trans. Amer. Math. Soc. 99 (1961), 212–240.Google Scholar
9. Conrad, P., The lattice of all convex l-subgroups of a lattice-ordered group, Czech. Math. J. 15 (1965), 101–123.Google Scholar
10. Conrad, P., Archimedean extensions of lattice-ordered groups, J. Indian Math. Soc. 80 (1966), 131–160.Google Scholar
11. Conrad, P., Harvey, J., and Holland, C., The Hahn embedding theorem for abelian latticeordered groups, Trans. Amer. Math. Soc. 108 (1963), 143–169.Google Scholar
12. Fuchs, L., Partially ordered algebraic systems (Pergamon Press, Oxford, 1963).Google Scholar
13. Holland, C., The interval topology of a certain l-group, Czech. Math. J. 15 (1965), 311–314.Google Scholar
14. Jakubik, J., Interval topology of an l-group, Colloq. Math. 11 (1963), 65–72.Google Scholar
15. Wolfenstein, S., Sur les groupes reticules archimédiennement complets, C. R. Acad. Sci. Paris 262 (1966), 813–816.Google Scholar
16. Wolfenstein, S., Extensions archimédiennes non-commutatives de groupes réticulés commutatifs, C. R. Acad. Sci. Paris 264 (1967), 1–4.Google Scholar
17. Wolk, E. S., On the interval topology of an l-group, Proc. Amer. Math. Soc. 12 (1961), 304–307.Google Scholar