Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-15T22:25:37.801Z Has data issue: false hasContentIssue false
  • English
  • Français

Arithmetic Invariants of Subdivision of Complexes

Published online by Cambridge University Press:  20 November 2018

C. T. C. Wall
C. T. C. Wall*
Affiliation:
Trinity College, Cambridge
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following problem was raised by M. Brown. Let K be a finite simplicial complex, of dimension n, with αi(K) simplexes of dimension i. Which of the linear combinations 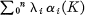have the property that they are unaltered by all stellar subdivisions of K? The most obvious invariant is the Euler characteristic; there are also some identities that hold for manifolds (2), so, if K is a manifold, they remain true on subdivision. We shall see that no other expressions are ever invariant, but if K resembles a manifold in codimensions ⩽2r (in a sense defined below) that r of the relations continue to hold.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 92 - 96
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Alexander, J. W., The combinatorial theory of complexes, Ann. of Math., 81 (1930), 292–320.Google Scholar
2. Klee, V., A combinatorial analogue of Poincaré's duality theorem, Can. J. Math., 16 (1964), 517–531.Google Scholar
3. Seifert, H. and Threlfall, W., Lehrbuch der Topologie (Leipzig, 1934).Google Scholar