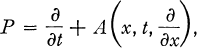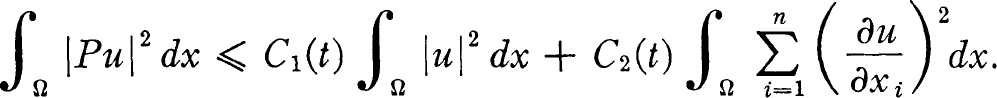Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, Lu-San
and
Kuroda, Tadashi
1966.
Unique Continuation for Parabolic Equations of Higher Order.
Nagoya Mathematical Journal,
Vol. 26,
Issue. ,
p.
115.
Ogawa, Hajimu
1967.
Lower Bounds for Solutions of Parabolic Differential Inequalities.
Canadian Journal of Mathematics,
Vol. 19,
Issue. ,
p.
667.
Ogawa, Hajimu
1970.
On the maximum rate of decay of solutions of parabolic differential inequalities.
Archive for Rational Mechanics and Analysis,
Vol. 38,
Issue. 3,
p.
173.
Ladas, G.
and
Lakshmikantham, V.
1971.
Lower bounds and uniqueness for solutions of evolution inequalities in a Hilbert space.
Archive for Rational Mechanics and Analysis,
Vol. 43,
Issue. 4,
p.
293.
Ladas, G.
and
Lakshmikantham, V.
1972.
Ordinary Differential Equations.
p.
473.
Ghidaglia, Jean-Michel
1986.
Long time behaviour of solutions of abstract inequalities: Applications to thermo-hydraulic and magnetohydrodynamic equations.
Journal of Differential Equations,
Vol. 61,
Issue. 2,
p.
268.
Pachpatte, B.G.
2000.
On Some Evolution Inequalities in a Hilbert Space.
Journal of Mathematical Analysis and Applications,
Vol. 246,
Issue. 1,
p.
122.
Del Santo, Daniele
and
Prizzi, Martino
2006.
On the absence of rapidly decaying solutions for parabolic operators whose coefficients are non-Lipschitz continuous in time.
Proceedings of the American Mathematical Society,
Vol. 135,
Issue. 2,
p.
383.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
535.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
765.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
233.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
1.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
989.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
345.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
423.
Qin, Yuming
2016.
Integral and Discrete Inequalities and Their Applications.
p.
885.