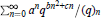Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hamamoto, T.
Kajiwara, K.
and
Witte, N. S.
2006.
Hypergeometric solutions to the q-Painleve equation of type $$ _ + _ ^{\prime })}^ $$.
International Mathematics Research Notices,
Gordon, Basil
and
McIntosh, Richard J.
2012.
Partitions, q-Series, and Modular Forms.
Vol. 23,
Issue. ,
p.
95.
Jockers, Hans
Mayr, Peter
Ninad, Urmi
and
Tabler, Alexander
2022.
BPS indices, modularity and perturbations in quantum K-theory.
Journal of High Energy Physics,
Vol. 2022,
Issue. 2,
Dixit, Atul
and
Kumar, Gaurav
2025.
The Rogers–Ramanujan dissection of a theta function.
Mathematische Annalen,
Vol. 393,
Issue. 1,
p.
667.