Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T10:35:13.010Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotics for Minimal Discrete Riesz Energy on Curves in ℝd

Published online by Cambridge University Press:  20 November 2018

A. Martínez-Finkelshtein ,
V. Maymeskul ,
E. A. Rakhmanov  and
E. B. Saff
A. Martínez-Finkelshtein
Affiliation:
Departamento de Estadística, y Matemática Aplicada, University of Almería, 04120 Almería, Spain e-mail: andrei@ual.es
V. Maymeskul
Affiliation:
Department of Mathematics, Vanderbilt University, Nashville, Tennessee 37240, USA e-mail: vmay@math.vanderbilt.edu
E. A. Rakhmanov
Affiliation:
Department of Mathematics, University of South Florida, Tampa, Florida 33620, USA e-mail: rakhmano@math.usf.edu
E. B. Saff
Affiliation:
Department of Mathematics, Vanderbilt University, Nashville, Tennessee 37240, USA e-mail: esaff@math.vanderbilt.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the $s$-energy 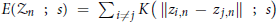$E({{Z}_{n}};\,s)={{\Sigma }_{i\ne j}}K(\parallel {{z}_{i,n}}\,-\,{{z}_{j,n}}\parallel \,;\,s)$ for point sets 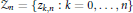$Zn\,=\,\{{{z}_{k,n}}\,:\,k\,=\,0,\,\ldots \,,\,n\} $ on certain compact sets $\Gamma $ in 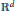${{\mathbb{R}}^{d}}$ having finite one-dimensional Hausdorff measure,where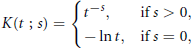

$$K(t;\,s)\,=\,\left\{ _{-\ln \,t,\,\,\,\text{if}\,s\,=\,0,\,}^{{{t}^{-s}},\,\,\,\,\,\,\,\text{if}\,s\,>\,0,} \right\}$$

is the Riesz kernel. Asymptotics for the minimum $s$-energy and the distribution of minimizing sequences of points is studied. In particular, we prove that, for 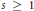$s\,\ge \,1$, the minimizing nodes for a rectifiable Jordan curve Γ distribute asymptotically uniformly with respect to arclength as 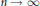$n\,\to \,\infty $.

Keywords

52A4031C20Riesz energyMinimal discrete energyRectifiable curvesBest-packing on curves
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 3 , 01 June 2004 , pp. 529 - 552
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] David, G. and Semmes, S., Singular integrals and rectifiable sets in Rn: Beyond Lipschitz graphs. Astérisque 193, 1991.Google Scholar
[2] Falconer, K. J., The Geometry of Fractal Sets. Cambridge Univ. Press, Cambridge, 1990.Google Scholar
[3] Hardin, D. and Saff, E. B., Minimal Riesz energy point configurations for rectifiable d-dimensionable manifolds. Manuscript, 2002.Google Scholar
[4] Kuijlaars, A. B. J. and Saff, E. B., Asymptotics of minimal discrete energy on the sphere. Trans. Amer. Math. Soc. (2) 350(1998), 523–538.Google Scholar
[5] Landkof, N. S., Foundations of Modern Potential Theory. Grundlehren der Mathematischen Wissenschaften, Springer-Verlag, Berlin, 1972.Google Scholar
[6] Lieb, E. H. and Loss, M., Analysis. Grad. Stud. Math. 14, Amer.Math. Soc., Providence, 1997.Google Scholar