Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T12:57:50.218Z Has data issue: false hasContentIssue false
  • English
  • Français

A Beurling Theorem for Generalized Hardy Spaces on a Multiply Connected Domain

Published online by Cambridge University Press:  20 November 2018

Yanni Chen ,
Don Hadwin ,
Zhe Liu  and
Eric Nordgren
Yanni Chen
Affiliation:
School of Mathematics and Information Science, Shaanxi Normal University, Xi'an, 710119, China email: yanni.chen@snnu.edu.cn
Don Hadwin
Affiliation:
Department of Mathematics, University of New Hampshire, Durham, NH 03824, USA email: don@unh.edu, ean@unh.edu
Zhe Liu
Affiliation:
Department of Mathematics, University of Central Florida, Orlando, FL 32816, USA email: zhe.liu@ucf.edu
Eric Nordgren
Affiliation:
Department of Mathematics, University of New Hampshire, Durham, NH 03824, USA email: don@unh.edu, ean@unh.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The object of this paper is to prove a version of the Beurling–Helson–Lowdenslager invariant subspace theorem for operators on certain Banach spaces of functions on a multiply connected domain in 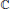$\mathbb{C}$. The norms for these spaces are either the usual Lebesgue and Hardy space norms or certain continuous gauge norms. In the Hardy space case the expected corollaries include the characterization of the cyclic vectors as the outer functions in this context, a demonstration that the set of analytic multiplication operators is maximal abelian and reflexive, and a determination of the closed operators that commute with all analytic multiplication operators.

Keywords

47L1030H10Beurling theoreminvariant subspacegeneralized Hardy spacegauge normmultiply connected domainForelli projectioninner-outer factorizationaffiliated operator
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 3 , 01 June 2018 , pp. 515 - 537
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Aleman, A. and Richter, S., Simply invariant subspaces of H2 of some multiply connected regions. Integral Equations Operator Theory 24(1996), no. 2, 127–155. http://dx.doi.org/10.1007/BF01193457 Google Scholar
[2] Aleman, A. and Richter, S., Erratum: “Simply invariant subspaces of H2 of some multiply connected regions”. Integral Equations Operator Theory 29(1997), no. 4, 501–504. http://dx.doi.Org/10.1007/BF01193814 Google Scholar
[3] Beurling, A., On two problems concerning linear transformations in Hilbert space. Acta Math. 81(1949), no. 17, 239–255.Google Scholar
[4] Chen, Y., Lebesgue and Hardy spaces for symmetric norms I. arxiv:1407.7920Google Scholar
[5] Chen, Y., A general Beurling-Helson-Lowdenslager theorem on the disk. Adv. in Appl. Math. 87(2017), 1–15. http://dx.doi.Org/10.1016/j.aam.2016.11.004 Google Scholar
[6] Conway, J. B., Functions of one complex variable II. Graduate Texts in Mathematics, 159, Springer-Verlag, New York, 1995. http://dx.doi.org/10.1007/978-1-4612-0817-4 Google Scholar
[7] Fisher, S. D., Function theory on planar domains. A second course in complex analysis. Pure and Applied Mathematics (New York), A Wiley-Interscience Publication, John Wiley & Sons, Inc., New York, 1983.Google Scholar
[8] Forelli, E., Bounded holomorphic functions and projections. Illinois J. Math. 10(1966), 367–380.Google Scholar
[9] Gamelin, T. W., Hp spaces and extremal functions in H1 . Trans. Amer. Math. Soc. 124(1966), 158–167. http://dx.doi.Org/10.2307/1994442 Google Scholar
[10] Gamelin, T. W., Uniform algebras. Prentice-Hall, Inc., Englewood Cliffs, N. J., 1969.Google Scholar
[11] Hadwin, D., Liu, Z., and Nordgren, E., Closed densely defined operators commuting with multiplications in a multiplier pair. Proc. Amer. Math. Soc. 141(2013), no. 9, 3093–3105. http://dx.doi.Org/10.1090/S0002-9939-2013-11753-3 Google Scholar
[12] Hadwin, D. and Nordgren, E., A general view of multipliers and composition operators. Linear Algebra Appl. 383(2004), 187–211. http://dx.doi.Org/10.1016/j.laa.2003.12.031 Google Scholar
[13] Hasumi, M., Invariant subspace theorems for finite Riemann surfaces. Canad. J. Math. 18(1966), 240–255. http://dx.doi.org/10.4153/CJM-1966-027-1 Google Scholar
[14] Helson, H. and Lowdenslager, D., Invariant subspaces. In: Proc. Internat. Sympos. Linear Spaces, (Jerusalem, 1960), Jerusalem Academic Press, Jerusalem; Pergamon, Oxford, 1961, pp. 251–262.Google Scholar
[15] Hitt, D., Invariant subspaces of ℋ2 of an annulus. Pacific J. Math. 134(1988), no. 1, 101–120. http://dx.doi.Org/10.2140/pjm.1988.134.101 Google Scholar
[16] Kuratowski, C., Théorèmes sur l'homotopie des fonctions continues de variable complexe et leurs rapports è la Théorie des fonctions analytiques. Fund. Math. 33(1945), 316–367. http://dx.doi.org/10.4064/fm-33-1-316-367 Google Scholar
[17] Nehari, Z., Conformal mapping. McGraw-Hill Book Co., Inc., New York, Toronto, London, 1952.Google Scholar
[18] Parreau, M., Sur les moyennes des fonctions harmoniques et analytiques et la classification des surfaces de Riemann. Ann. Inst. Fourier Grenoble 3(1951), 103–197. http://dx.doi.Org/10.5802/aif.37 Google Scholar
[19] Royden, H. L., Invariant subspaces of ℋ p for multiply connected regions. Pacific J. Math. 134(1988), no. 1, 151–172. http://dx.doi.org/10.2140/pjm.1988.134.151 Google Scholar
[20] Rudin, W., Analytic functions of class Hp . Trans. Amer. Math. Soc. 78(1955), 46–66. http://dx.doi.Org/10.2307/1992948 Google Scholar
[21] Rudol, K., Some results related to Beurling's theorem. Univ. Iagel. Acta Math., 38(2000), 289–298.Google Scholar
[22] Saks, S. and Zygmund, A., Analytic functions. Third ed., Elsevier Publishing Co., Amsterdam-London-New York; PWN—Polish Scientific Publishers, Warsaw, 1971.Google Scholar
[23] Sarason, D., The Hp spaces of an annulus. Mem. Amer. Math. Soc. 56(1965).Google Scholar
[24] Tsuji, M., Potential theory in modern function theory. Maruzen Co., Ltd., Tokyo, 1959.Google Scholar
[25] Voichick, M., Ideals and invariant subspaces of analytic functions. Trans. Amer. Math. Soc. 111(1964), 493–512. http://dx.doi.org/10.1090/S0002-9947-1964-0160920-5 Google Scholar
[26] Voichick, M., Invariant subspaces on Riemann surfaces. Canad. J. Math. 18(1966), 399–403. http://dx.doi.org/10.4153/CJM-1966-042-8 Google Scholar