Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T03:59:32.144Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bishop-Phelps-Bollobàs Property for Compact Operators

Published online by Cambridge University Press:  20 November 2018

Sheldon Dantas ,
Domingo García ,
Manuel Maestre  and
Miguel Martín
Sheldon Dantas
Affiliation:
Departamento de Análisis Matemático, Universidad de Valencia, Doctor Moliner 50, 46100 Burjasot (Valencia), Spain e-mail: sheldon.dantas@uv.esdomingo.garcia@uv.esmanuel.maestre@uv.es
Domingo García
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain e-mail: mmartins@ugr.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

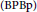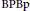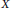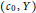We study the Bishop-Phelps-Bollobàs property $\left( \text{BPBp} \right)$ for compact operators. We present some abstract techniques that allow us to carry the $\text{BPBp}$ for compact operators from sequence spaces to function spaces. As main applications, we prove the following results. Let $X$ and $Y$ be Banach spaces. If $\left( {{c}_{0}},Y \right)$ has the 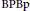$\text{BPBp}$ for compact operators, then so do 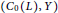$\left( {{C}_{0}}\left( L \right),Y \right)$ for every locally compact Hausdorff topological space $L$ and 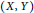$\left( X,\,Y \right)$ whenever 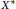${{X}^{*}}$ is isometrically isomorphic to 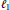${{\ell }_{1}}$. If 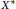${{X}^{*}}$ has the Radon-Nikodým property and $\left( {{\ell }_{1}}\left( X \right),\,Y \right)$ has the 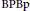$\text{BPBp}$ for compact operators, then so does 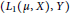$\left( {{L}_{1}}\left( \mu ,X \right),\,\,Y \right)$ for every positive measure $\mu $; as a consequence, 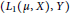$\left( {{L}_{1}}\left( \mu ,X \right),\,\,Y \right)$ has the 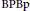$\text{BPBp}$ for compact operators when 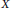$X$ and $Y$ are finite-dimensional or $Y$ is a Hilbert space and 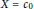$X={{c}_{0}}$ or 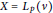$X={{L}_{p}}\left( v \right)$ for any positive measure $v$ and 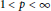$1\,<\,p\,<\,\infty $. For 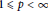$1\,\le p\,<\,\infty$, if 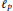$\left( X,{{l}_{p}}(Y) \right)$ has the 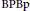$\text{BPBp}$ for compact operators, then so does 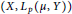$\left( X,{{L}_{p}}\left( \mu ,\,Y \right) \right)$ for every positive measure $\mu $ such that 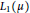${{L}_{1}}\left( \mu \right)$ is infinite-dimensional. If 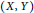$\left( X,\,Y \right)$ has the 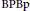$\text{BPBp}$ for compact operators, then so do 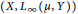$\left( X,\,{{L}_{\infty }}\left( \mu ,\,\,Y \right) \right)$ for every $\sigma $-finite positive measure $\mu $ and 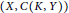$\left( X,\,C\left( K,\,Y \right) \right)$ for every compact Hausdorff topological space 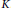$K$.

Keywords

46B0446B2046B2846B2546B40Bishop–Phelps theoremBishop–Phelps–Bollobás propertynorm attaining operatorcompact operator
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 1 , 01 February 2018 , pp. 53 - 57
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Acosta, M. D., Denseness of norm attaining mappings, Rev. R. Acad. Cien. Exactas Ffs. Nat. Ser. A Mat. 100(2006), 9–30.Google Scholar
[2] Acosta, M. D., The Bishop-Phelps-Bollobàs property for operators on C(K). Banach J. Math. Anal. 10(2016), no. 2,307–319.http://dx.doi.org/10.1215/17358787-3492875 Google Scholar
[3] Acosta, M. D., Aron, R. M., Garcia, D., and Maestre, M., The Bishop-Phelps-Bollobds theorem for operators. J. Funct. Anal. 294(2008), 2780–2899.http://dx.doi.org/10.1016/j.jfa.2008.02.014 Google Scholar
[4] Acosta, M. D., Becerra-Guerrero, J., Choi, Y. S., Ciesielski, M., Kim, S. K., Lee, H. J., Lourenço, M. L., and Martn, M., The Bishop-Phelps-Bollobds property for operators between spaces of continuous functions. Nonlinear Anal. 95(2014), 323–332. http://dx.doi.Org/10.1016/j.na.2O13.09.011 Google Scholar
[5] Acosta, M. D., Becerra-Guerrero, J., Garcia, D., Kim, S. K., and Maestre, M., The Bishop-Phelps-Bollobds theorem for bilinear forms. Tran. Amer. Math. Soc, 11(2013), 5911–5932.http://dx.doi.Org/10.1090/S0002-9947-2013-05881-3 Google Scholar
[6] Acosta, M. D., Becerra-Guerrero, J., Garcia, D., Kim, S. K. and Maestre, M., Bishop-Phelps-Bollobàs property for certain spaces of operators. J. Math. Anal. Appl. 414 (2014), 532–545.http://dx.doi.Org/10.1016/j.jmaa.2O13.12.056 Google Scholar
[7] Acosta, M. D., Garcia, D., Kim, S. K. and Maestre, M., Bishop-Phelps-Bollobàs property for operators from C0 into some Banach spaces. J. Math. Anal. Appl. 445(2017), 1188–1199.http://dx.doi.Org/10.1016/j.jmaa.2016.02.029 Google Scholar
[8] Aron, R. M., Choi, Y. S., Kim, S. K., Lee, H. J., and Martin, M., The Bishop-Phelps-Bollobàs version of Lindenstrauss properties A and B. Trans. Amer. Math. Soc. 367(2015), 6085–6101. http://dx.doi.org/10.1090/S0002-9947-2015-06551-9 Google Scholar
[9] Bishop, E. and Phelps, R. R., A proof that every Banach space is subreflexive. Bull. Amer. Math. Soc. 67(1961), 97–98.http://dx.doi.org/10.1090/S0002-9904-1961-10514-4 Google Scholar
[10] Bollobàs, B., An extension to the Theorem of Bishop and Phelps. Bull. London Math. Soc. 2(1970), 181–182.http://dx.doi.Org/10.1112/blms/2.2.181 Google Scholar
[11] Cascales, B., Guirao, J., and Kadets, V., A Bishop-Phelps-Bollobàs type theorem for uniform algebras. Adv. Math. 240(2013), 370–382.http://dx.doi.Org/10.1016/j.aim.2013.03.005 Google Scholar
[12] Cembranos, P. and Mendoza, J., Banach spaces of vector-valued functions. Lecture Notes in Mathematics, 1676, Springer-Verlag, Berlin, 1997.http://dx.doi.Org/10.1007/BFb0096765 Google Scholar
[13] Cho, D. H. and Choi, Y. S., The Bishop-Phelps-Bollobàs theorem on bounded closed convex sets. J. London Math. Soc. 93(2016), 502–518. http://dx.doi.Org/10.1112/jlms/jdw002 Google Scholar
[14] Choi, Y. S. and Kim, S. K., The Bishop-Phelps-Bollobàs theorem for operators from Li(fi) to Banach spaces with the Radon-Nikodym property. J. Funct. Anal. 261(2011), 1446–1456.http://dx.doi.Org/10.1016/j.jfa.2O11.05.007 Google Scholar
[15] Choi, Y S., Kim, S. K., Lee, H. J., and Martin, M., The Bishop-Phelps-Bollobàs theorem for operators on Ll(μ). J. Funct. Anal. 267(2014), no. 1, 214–242.http://dx.doi.org/10.1016/j.jfa.2O14.04.008 Google Scholar
[16] Diestel, J. and Uhl, J. J., Vector measures. Mathematical Surveys, 15, Americal Mathematical Society, Providence, RI. 1977.Google Scholar
[17] Gasparis, I., On contractively complemented subspaces of separable Ll-preduals. Israel J. Math. 128(2002), 77–92.http://dx.doi.org/10.1007/BF02785419 Google Scholar
[18] Johnson, J. and Wolfe, J., Norm attaining operators. Studia Math. 65(1979), 7–19.Google Scholar
[19] Johnson, W. B., Finite-dimensional Schauder decompositions in πλ and dual πλ spaces. Illinois J. Math. 14(1970), 642–647.Google Scholar
[20] Kim, S. K. and Lee, H. J., Uniform convexity and the Bishop-Phelps-Bollbàs property. Canad. J. Math. 66(2014), 373–386.http://dx.d0i.0rg/10.4153/CJM-2O13-009-2 Google Scholar
[21] Kim, S. K. and Lee, H. J., The Bishop-Phelps-Bollobàs property for operators from C(K) to uniformly convex spaces. J. Math. Anal. Appl. 421(2015), 51–58.http://dx.doi.Org/10.1016/j.jmaa.2O14.06.081 Google Scholar
[22] Kim, S. K., Lee, H. J., and Martin, M., The Bishop-Phelps-Bollobàs theorem for operators from sums. J. Math. Anal. Appl. 428(2015), 920–929.http://dx.doi.Org/10.1016/j.jmaa.2015.03.057 Google Scholar
[23] Lindenstrauss, J., On operators which attain their norm. Isr. J. Math. 1(1963), 139–148.http://dx.doi.org/10.1007/BF02759700 Google Scholar
[24] Martin, M., Norm-attaining compact operators. J. Funct. Anal. 267(2014), 1585–1592.http://dx.doi.Org/10.1016/j.jfa.2O14.05.019 Google Scholar
[25] Martin, M., The version for compact operators of Lindenstrauss properties A and B. Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Math. RACSAM 110(2016), 269–284.http://dx.doi.Org/10.1007/s13398-01 5-0219-5 Google Scholar
[26] Schachermayer, W., Norm attaining operators on some classical Banach spaces. Pacific J. Math. 105(1983), 427–438.http://dx.doi.org/10.2140/pjm.1983.105.427 Google Scholar