BMO-Estimates for Maximal Operators via Approximations of the Identity with Non-Doubling Measures

Abstract

Let $\mu $ be a nonnegative Radon measure on 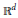${{\mathbb{R}}^{d}}$ that satisfies the growth condition that there exist constants 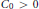${{C}_{0}}\,>\,0$ and 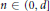$n\,\in \,(0,\,d]$ such that for all 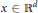$x\,\in \,{{\mathbb{R}}^{d}}$ and 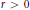$r\,>\,0$, 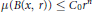$\mu \left( B\left( x,\,r \right) \right)\,\le \,{{C}_{0}}{{r}^{n}}$, where 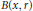$B(x,\,r)$ is the open ball centered at $x$ and having radius $r$. In this paper, the authors prove that if 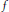$f$ belongs to the 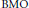$\text{BMO}$-type space 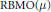$\text{RBMO(}\mu \text{)}$ of Tolsa, then the homogeneous maximal function 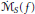${{\dot{\mathcal{M}}}_{s}}\left( f \right)$ (when 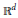${{\mathbb{R}}^{d}}$ is not an initial cube) and the inhomogeneous maximal function 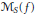${{\overset{{}}{\mathop{\mathcal{M}}}\,}_{s}}\left( f \right)$ (when 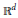${{\mathbb{R}}^{d}}$ is an initial cube) associated with a given approximation of the identity $S $ of Tolsa are either infinite everywhere or finite almost everywhere, and in the latter case, 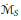${{\dot{\mathcal{M}}}_{s}}$ and 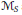${{\mathcal{M}}_{s}}$ are bounded from 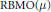$\text{RBMO(}\mu \text{)}$ to the 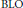$\text{BLO}$-type space 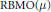$\text{RBMO(}\mu \text{)}$. The authors also prove that the inhomogeneous maximal operator 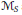${{\mathcal{M}}_{s}}$ is bounded from the local 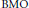$\text{BMO}$-type space 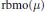$\text{rbmo(}\mu \text{)}$ to the local 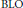$\text{BLO}$-type space 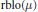$\text{rblo(}\mu \text{)}$.