Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T23:12:02.076Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bombieri–Vinogradov Theorem on Higher Rank Groups and its Applications

Part of: Exponential sums and character sums Multiplicative number theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 March 2019

Yujiao Jiang  and
Guangshi Lü
Yujiao Jiang
Affiliation:
School of Mathematics and Statistics, Shandong University, Weihai, Weihai, Shandong 264209, China Email: yujiaoj@hotmail.com
Guangshi Lü
Affiliation:
School of Mathematics, Shandong University, Jinan, Shandong 250100, China Email: gslv@sdu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the analogue of the Bombieri–Vinogradov theorem for 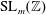$\operatorname{SL}_{m}(\mathbb{Z})$ Hecke–Maass form 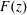$F(z)$. In particular, for 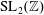$\operatorname{SL}_{2}(\mathbb{Z})$ holomorphic or Maass Hecke eigenforms, symmetric-square lifts of holomorphic Hecke eigenforms on 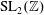$\operatorname{SL}_{2}(\mathbb{Z})$, and 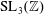$\operatorname{SL}_{3}(\mathbb{Z})$ Maass Hecke eigenforms under the Ramanujan conjecture, the levels of distribution are all equal to 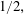$1/2,$ which is as strong as the Bombieri–Vinogradov theorem. As an application, we study an automorphic version of Titchmarch’s divisor problem; namely for 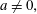$a\neq 0,$

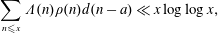$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D6EC}(n)\unicode[STIX]{x1D70C}(n)d(n-a)\ll x\log \log x,\end{eqnarray}$$
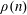where $\unicode[STIX]{x1D70C}(n)$ are Fourier coefficients 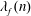$\unicode[STIX]{x1D706}_{f}(n)$ of a holomorphic Hecke eigenform 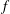$f$ for 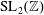$\operatorname{SL}_{2}(\mathbb{Z})$ or Fourier coefficients 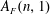$A_{F}(n,1)$ of its symmetric-square lift 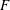$F$. Further, as a consequence, we get an asymptotic formula
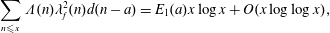$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D6EC}(n)\unicode[STIX]{x1D706}_{f}^{2}(n)d(n-a)=E_{1}(a)x\log x+O(x\log \log x),\end{eqnarray}$$
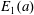 where $E_{1}(a)$ is a constant depending on $a$. Moreover, we also consider the asymptotic orthogonality of the Möbius function against the arithmetic function 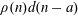$\unicode[STIX]{x1D70C}(n)d(n-a)$.

Keywords

Bombieri–Vinogradov theoremFourier coefficientMaass formshifted convolution sumprime

MSC classification

Primary: 11F30: Fourier coefficients of automorphic forms
Secondary: 11L05: Gauss and Kloosterman sums; generalizations 11L20: Sums over primes 11N37: Asymptotic results on arithmetic functions 11N75: Applications of automorphic functions and forms to multiplicative problems
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 4 , August 2020 , pp. 928 - 966
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author Y. J. is supported by the China Postdoctoral Science Foundation (No. 2017M620285), and G. L. is supported in part by NSFC (Nos. 11771252, 11531008), IRT16R43, and Taishan Scholars Project.

References

Banks, W. D., Twisted symmetric-square L-functions and the nonexistence of siegel zeros on GL(3). Duke Math. J. 87(1997), 343–354. https://doi.org/10.1215/S0012-7094-97-08713-5Google Scholar
Barnet-Lamb, T., Geraghty, D., Harris, M., and Taylor, R., A family of Calabi–Yau varieties and potential automorphy II. Publ. Res. Inst. Math. Sci. 47(2011), 29–98. https://doi.org/10.2977/PRIMS/31Google Scholar
Barthel, L. and Ramakrishnan, D., A nonvanishing result for twists of L-functions of GL(n). Duke Math. J. 74(1994), 81–700. https://doi.org/10.1215/S0012-7094-94-07425-5Google Scholar
Bombieri, E., Friedlander, J. B., and Iwaniec, H., Primes in arithmetic progressions to large moduli. Acta Math. 156(1986), 203–251. https://doi.org/10.1007/BF02399204Google Scholar
Bump, D., Automorphic forms and representations. Cambridge Studies in Advanced Mathematics, 55, Cambridge University Press, Cambridge, 1997. https://doi.org/10.1017/CBO9780511609572Google Scholar
Deligne, P., La conjecture de Weil. I. Inst. Hautes Études Sci. Publ. Math. 43(1974), 273–307.Google Scholar
Erdös, P. and Szekeres, G., Über die Anzahl der Abelschen Gruppen gegebener Ordnung und über ein verwandtes zahlentheoretisches Problem. Acta Sci. Math. (Szeged) 7(1935), 95–102.Google Scholar
Fouvry, É., Sur le probléme des diviseurs de Titchmarsh. J. Reine Angew. Math. 357(1985), 51–76. https://doi.org/10.1515/crll.1985.357.51Google Scholar
Fouvry, É. and Ganguly, S., Strong orthogonality between the Möbius function, additive characters and Fourier coefficients of cusp forms. Compos. Math. 150(2014), 763–797. https://doi.org/10.1112/S0010437X13007732Google Scholar
Godber, D., Additive twists of Fourier coefficients of modular forms. J. Number Theory 133(2013), 83–104. https://doi.org/10.1016/j.jnt.2012.07.010Google Scholar
Goldfeld, D., Automorphic forms and L-functions for the group GL(n, ℝ). (Cambridge Studies in Advanced Mathematics, 99), Cambridge University Press, Cambridge, 2006. https://doi.org/10.1017/CBO9780511542923Google Scholar
Goldfeld, D. and Li, X., The Voronoi formula for GL(n, ℝ). Int. Math. Res. Not. IMRN(2008), Art. ID rnm144.Google Scholar
Good, A., Cusp forms and eigenfunctions of the Laplacian. Math. Ann. 255(1981), 523–548. https://doi.org/10.1007/BF01451932Google Scholar
Halberstam, H., Footnote to the Titchmarsh-Linnik divisor problem. Proc. Amer. Math. Soc. 18(1967), 187–188. https://doi.org/10.2307/2035254Google Scholar
Hoffstein, J. and Ramakrishnan, D., Siegel zeros and cusp forms. Internat. Math. Res. Notices IMRN 1995 no. 6, 279–308. https://doi.org/10.1155/S1073792895000225Google Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory. (American Mathematical Society Colloquium Publications, 53), American Mathematical Society, Providence, RI, 2004. https://doi.org/10.1090/coll/053Google Scholar
Jiang, Y. and Lü, G., On sums of Fourier coefficients of Maass cusp forms. Int. J. Number Theory 13(2017), 1233–1243. https://doi.org/10.1142/S179304211750066XGoogle Scholar
Jiang, Y. and Lü, G., Exponential sums formed with the von Mangoldt function and Fourier coefficients of GL(m) automorphic forms. Monatsh. Math. 184(2017), 539–561. https://doi.org/10.1007/s00605-017-1068-4Google Scholar
Jiang, Y., Lü, G., and Yan, X., Mean value theorem connected with Fourier coefficients of Hecke-Maass forms for sL(m, ℤ). Math. Proc. Cambridge Philos. Soc. 161(2016), 339–356. https://doi.org/10.1017/S030500411600027XGoogle Scholar
Kim, H. H., Functoriality for the exterior square of GL4 and the symmetric fourth of GL2. J. Amer. Math. Soc. 16(2003), 139–183.Google Scholar
Kim, H. H., A note on Fourier coefficients of cusp forms on GLn. Forum Math. 18(2006), 115–119. https://doi.org/10.1515/FORUM.2006.007Google Scholar
Kim, H. H. and Shahidi, F., Functorial products for GL2 × GL3 and the symmetric cube for GL2. Ann. of Math. 155(2002), 837–893. https://doi.org/10.2307/3062134Google Scholar
Kim, H. H. and Shahidi, F., Cuspidality of symmetric powers with applications. Duke Math. J. 112 177–197. https://doi.org/10.1215/S0012-9074-02-11215-0Google Scholar
Kıral, E. M. and Zhou, F., The Voronoi formula and double Dirichlet series. Algebra Number Theory 10(2016), 2267–2286. https://doi.org/10.2140/ant.2016.10.2267Google Scholar
Linnik, Ju. V., The dispersion method in binary additive problems. Translated by S. Schuur. American Mathematical Society, Providence, RI, 1963.Google Scholar
Liu, J. and Sarnak, P., The Möbius function and distal flows. Duke Math. J. 164(2015), 1353–1399. https://doi.org/10.1215/00127094-2916213Google Scholar
Luo, W., Rudnick, Z., and Sarnak, P., Automorphic forms, automorphic representations, and arithmetic (Fort Worth, TX, 1996). (Proc. Sympos. Pure Math., 66), Amer. Math. Soc., Providence, RI, 1999, pp. 301–310.Google Scholar
Lü, G., Shifted convolution sums of Fourier coefficients with divisor functions. Acta Math. Hungar. 146(2015), 86–97. https://doi.org/10.1007/s10474-015-0499-4Google Scholar
Meurman, T., On exponential sums involving the Fourier coefficients of Maass wave forms. J. Reine Angew. Math. 384(1988), 192–207. https://doi.org/10.1515/crll.1988.384.192Google Scholar
Meurman, T., Number theory, Vol. I (Budapest, 1987). (Colloq. Math. Soc. János Bolyai, 51), North-Holland, Amsterdam, 1990, pp. 325–354.Google Scholar
Miller, S. D. and Schmid, W., Automorphic distributions, L-functions, and Voronoi summation for GL(3). Ann. of Math. (2) 164(2006), 423–488. https://doi.org/10.4007/annals.2006.164.423Google Scholar
Miller, S. D. and Schmid, W., Geometry and analysis, no. 2. (Adv. Lect. Math., 18), Int. Press, Somerville, MA, 2011, pp. 173–224.Google Scholar
Molteni, G., L-functions: Siegel-type theorems and structure theorems. Ph. D. thesis, University of Milan, Milan, 1999. 141, 1999.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Classical theory. (Cambridge Studies in Advanced Mathematics, 97), Cambridge University Press, Cambridge, 2007.Google Scholar
Perelli, A., Seminar on number theory, 1983–1984 (Talence, 1983/1984), Exp. No. 25, 9. Univ. Bordeaux I, Talence, 1984.Google Scholar
Ren, X. and Ye, Y., Resonance and rapid decay of exponential sums of Fourier coefficients of a Maass form for GLm(ℤ). Sci. China Math. 58(2015), 2105–2124. https://doi.org/10.1007/s11425-014-4955-3Google Scholar
Rodriquez, G., Sul problema dei divisori di Titchmarsh. Boll. Un. Mat. Ital. 20(1965), 358–366.Google Scholar
Rudnick, Z. and Sarnak, P., Zeros of principal L-functions and random matrix theory. Duke Math. J. 81(1996), 269–322. https://doi.org/10.1215/S0012-7094-96-08115-6Google Scholar
Sarnak, P., Three lectures on the Möbius function, randomness and dynamics. http://publications.ias.edu/sarnak/2010 (accessed June 20, 2016).Google Scholar
Shiu, P., A Brun-Titchmarsh theorem for multiplicative functions. J. Reine Angew. Math. 313(1980), 161–170. https://doi.org/10.1515/crll.1980.313.161Google Scholar
Smith, R. A., Fourier coefficients of modular forms over arithmetic progressions. I, II, With remarks by M. R. Murty. C. R. Math. Rep. Acad. Sci. Canada 15(1993), 85–90, 91–98Google Scholar
Titchmarsh, E. C., A divisor problem. Rend. Circ. Mat. Palermo 54(1930), 414–429.Google Scholar
Titchmarsh, E. C., A divisor problem, Correction. Rend. Circ. Mat. Palermo 57(1933), 478–479.Google Scholar
Vaughan, R. C., An elementary method in prime number theory. Acta Arithmetica 37(1980), 111–115. https://doi.org/10.4064/aa-37-1-111-115Google Scholar
Wang, Z., Möbius disjointness for analytic skew products. Invent. Math. 209(2017), 175–196.Google Scholar
Weinstein, L., The hyper-Kloosterman sum. Enseign. Math. 27(1981), 29–40.Google Scholar