Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-15T11:26:28.090Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary Behavior and Quasi-Normality of Finitely Valent Holomorphic Functions

Published online by Cambridge University Press:  20 November 2018

David C. Haddad
David C. Haddad*
Affiliation:
West Virginia College of Graduate Studies, Institute, West Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

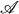A function denned in a domain D is n-valent in D if f(z) — w0 has at most n zeros in D for each complex number w0. Let denote the class of nonconstant, holomorphic functions f in the unit disc that are n-valent in each component of the set . MacLane's class is the class of nonconstant, holomorphic functions in the unit disc that have asymptotic values at a dense subset of |z| = 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 25 , Issue 4 , August 1973 , pp. 812 - 819
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Bagemihl, F. and Seidel, W., Koebe arcs and Fatou points of normal functions, Comment. Math. Helv. 36 (1962), 9–18.Google Scholar
2. Haddad, D. C., Asymptotic values of finitely valent functions, Duke Math. J. 89 (1972), 362–367.Google Scholar
3. Lehto, O. and Virtanen, K. I., Boundary behaviour and normal meromorphic functions, Acta. Math. 97 (1957), 46–65.Google Scholar
4. MacLane, G. R., Asymptotic values of holomorphic functions, Rice University Studies J±9, No. 1 (1963).Google Scholar
5. Montel, P., Leçons sur les familles normales de fonctions analytiques et leurs applications (Gauthier-Villars, Paris, 1927).Google Scholar