Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T20:30:53.995Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary Quotient 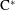$\text{C}^{\ast }$-algebras of Products of Odometers

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  07 January 2019

Hui Li  and
Dilian Yang
Hui Li
Affiliation:
Research Center for Operator Algebras and Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, Department of Mathematics, East China Normal University, 3663 Zhongshan North Road, Putuo District, Shanghai 200062, China Email: lihui8605@hotmail.com
Dilian Yang
Affiliation:
Department of Mathematics and Statistics, University of Windsor, Windsor, ON, N9B 3P4 Email: dyang@uwindsor.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the boun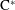dary quotient $\text{C}^{\ast }$-algebras associated with products of odometers. One of our main results shows that the boundary quotient 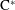$\text{C}^{\ast }$-algebra of the standard product of 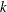$k$ odometers over 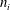$n_{i}$-letter alphabets 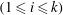$(1\leqslant i\leqslant k)$ is always nuclear, and that it is a UCT Kirchberg algebra if and only if 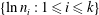$\{\ln n_{i}:1\leqslant i\leqslant k\}$ is rationally independent, if and only if the associated single-vertex 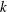$k$-graph 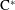$\text{C}^{\ast }$-algebra is simple. To achieve this, one of our main steps is to construct a topological 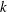$k$-graph such that its associated Cuntz–Pimsner 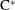$\text{C}^{\ast }$-algebra is isomorphic to the boundary quotient 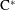$\text{C}^{\ast }$-algebra. Some relations between the boundary quotient 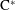$\text{C}^{\ast }$-algebra and the 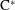$\text{C}^{\ast }$-algebra 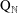$\text{Q}_{\mathbb{N}}$ introduced by Cuntz are also investigated.

Keywords

C∗ -algebrasemigroupodometertopological k-graphproduct systemZappa–Szép product

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 1 , February 2019 , pp. 183 - 212
Copyright
© Canadian Mathematical Society 2017 

Footnotes

Author H. L. was partially supported by Research Center for Operator Algebras of East China Normal University and was partially supported by Science and Technology Commission of Shanghai Municipality (STCSM), grant No. 13dz2260400. Author D. Y. was partially supported by an NSERC Discovery Grant 808235.

References

Afsar, Z., Brownlowe, N., Larsen, N. S., and Stammeier, N., Equilibrium states on right LCM semigroup C∗-algebras. arxiv:1611.01052.Google Scholar
Barlak, S., Omland, T., and Stammeier, N., On the K-theory of C∗-algebras arising from integral dynamics . Ergodic Theory Dynam. Systems, to appear. arxiv:1512.04496.Google Scholar
Brin, M. G., On the Zappa–Szép product . Comm. Algebra 33(2005), 393–424. https://doi.org/10.1081/AGB-200047404.Google Scholar
Brown, J., Clark, L.O., Farthing, C., and Sims, A., Simplicity of algebras associated to étale groupoids . Semigroup Forum 88(2014), 433–452. https://doi.org/10.1007/s00233-013-9546-z.Google Scholar
Brown, J. H., Nagy, G., and Reznikoff, S., A generalized Cuntz-Krieger uniqueness theorem for higher-rank graphs . J. Funct. Anal. 266(2014), 2590–2609. https://doi.org/10.1016/j.jfa.2013.08.020.Google Scholar
Brownlowe, N., Larsen, N. S., and Stammeier, N., On C∗-algebras associated to right LCM semigroups . Trans. Amer. Math. Soc. 369(2017), 31–68. https://doi.org/10.1090/tran/6638.Google Scholar
Brownlowe, N., Ramagge, J., Robertson, D., and Whittaker, M. F., Zappa–Szép products of semigroups and their C∗-algebras . J. Funct. Anal. 266(2014), 3937–3967. https://doi.org/10.1016/j.jfa.2013.12.025.Google Scholar
Carlsen, T. M., Larsen, N. S., Sims, A., and Vittadello, S. T., Co-universal algebras associated to product systems, and gauge-invariant uniqueness theorems . Proc. Lond. Math. Soc. (3) 103(2011), 563–600. https://doi.org/10.1112/plms/pdq028.Google Scholar
Cuntz, J., C∗-algebras associated with the ax + b-semigroup over ℕ . In: K-theory and noncommutative geometry, EMS Ser. Congr. Rep., Eur. Math. Soc., Zürich, 2008, pp. 201–215. https://doi.org/10.4171/060-1/8.Google Scholar
Davidson, K. R., Power, S. C., and Yang, D., Atomic representations of rank 2 graph algebras . J. Funct. Anal. 255(2008), 819–853. https://doi.org/10.1016/j.jfa.2008.05.008.Google Scholar
Davidson, K. R., Power, S. C., and Yang, D., Dilation theory for rank 2 graph algebras . J. Operator Theory 63(2010), 245–270.Google Scholar
Davidson, K. R. and Yang, D., Periodicity in rank 2 graph algebras . Canad. J. Math. 61(2009), 1239–1261. https://doi.org/10.4153/CJM-2009-058-0.Google Scholar
Davidson, K. R. and Yang, D., Representations of higher rank graph algebras . New York J. Math. 15(2009), 169–198.Google Scholar
Fowler, N. J., Discrete product systems of Hilbert bimodules . Pacific J. Math. 204(2002), 335–375. https://doi.org/10.2140/pjm.2002.204.335.Google Scholar
Fowler, N. J., Muhly, P. S., and Raeburn, I., Representations of Cuntz-Pimsner algebras . Indiana Univ. Math. J. 52(2003), 569–605. https://doi.org/10.1512/iumj.2003.52.2125.Google Scholar
Fowler, N. J. and Sims, A., Product systems over right-angled Artin semigroups . Trans. Amer. Math. Soc. 354(2002), 1487–1509. https://doi.org/10.1090/S0002-9947-01-02911-7.Google Scholar
Kaliszewski, S., Omland, T., and Quigg, J., Cuntz-Li algebras from a-adic numbers . Rev. Roumaine Math. Pures Appl. 59(2014), 331–370.Google Scholar
Katsura, T., A class of C∗-algebras generalizing both graph algebras and homeomorphism C∗-algebras I. Fundamental results . Trans. Amer. Math. Soc. 356(2004), 4287–4322. https://doi.org/10.1090/S0002-9947-04-03636-0.Google Scholar
Katsura, T., On C∗-algebras associated with C∗-correspondences . J. Funct. Anal. 217(2004), 366–401. https://doi.org/10.1016/j.jfa.2004.03.010.Google Scholar
Katsura, T., A class of C∗-algebras generalizing both graph algebras and homeomorphism C∗-algebras. IV. Pure infiniteness . J. Funct. Anal. 254(2008), 1161–1187. https://doi.org/10.1016/j.jfa.2007.11.014.Google Scholar
Kumjian, A. and Pask, D., Higher rank graph C∗-algebras . New York J. Math. 6(2000), 1–20.Google Scholar
Laca, M., Raeburn, I., Ramagge, J., and Whittaker, M. F., Equilibrium states on the Cuntz–Pimsner algebras of self-similar actions . J. Funct. Anal. 266(2014), 6619–6661. https://doi.org/10.1016/j.jfa.2014.03.003.Google Scholar
Larsen, N. S. and Li, X., The 2-adic ring C∗-algebra of the integers and its representations . J. Funct. Anal. 262(2012), 1392–1426. https://doi.org/10.1016/j.jfa.2011.11.008.Google Scholar
Li, X., Semigroup C∗-algebras and amenability of semigroups . J. Funct. Anal. 262(2012), 4302–4340. https://doi.org/10.1016/j.jfa.2012.02.020.Google Scholar
Li, X., Nuclearity of semigroup C∗-algebras and the connection to amenability . Adv. Math. 244(2013), 626–662. https://doi.org/10.1016/j.aim.2013.05.016.Google Scholar
Nekrashevych, V., Self-similar groups . Mathematical Surveys and Monographs, 117, American Mathematical Society, Providence, RI, 2005. https://doi.org/10.1090/surv/117.Google Scholar
Phillips, N. C., A Classification theorem for nuclear purely infinite simple C∗-algebras . Doc. Math. 5(2000), 49–114.Google Scholar
Pimsner, M. V., A class of C∗-algebras generalizing both Cuntz-Krieger algebras and crossed products by Z . In: Free probability theory (Waterloo, ON, 1995), Fields Inst. Commun., 12, American Mathematical Society, Providence, RI, 1997, pp. 189–212.Google Scholar
Raeburn, I., Sims, A., and Yeend, T., The C∗-algebras of finitely aligned higher-rank graphs . J. Funct. Anal. 213(2004), 206–240. https://doi.org/10.1016/j.jfa.2003.10.014.Google Scholar
Renault, J., A groupoid approach to C∗-algebras . Lecture Notes in Mathematics, 793, Springer, Berlin, 1980.Google Scholar
Renault, J. N., Sims, A., Williams, D. P., and Yeend, T., Uniqueness theorems for topological higher-rank graph C∗-algebras . Proc. Amer. Math. Soc., to appear. arxiv:0906.0829v3.Google Scholar
Rosenberg, J. and Schochet, C., The Künneth theorem and the universal coefficient theorem for Kasparov’s generalized K-functor . Duke Math. J. 55(1987), 431–474. https://doi.org/10.1215/S0012-7094-87-05524-4.Google Scholar
Sims, A. and Yeend, T., C∗-algebras associated to product systems of Hilbert bimodules . J. Operator Theory 64(2010), 349–376.Google Scholar
Stammeier, N., On C∗-algebras of irreversible algebraic dynamical systems . J. Funct. Anal. 269(2015), 1136–1179. https://doi.org/10.1016/j.jfa.2015.02.005.Google Scholar
Stammeier, N., A boundary quotient diagram for right LCM semigroups . Semigroup Forum, to appear. arxiv:1604.03172.Google Scholar
Starling, C., Boundary quotients of C∗-algebras of right LCM semigroups . J. Funct. Anal. 268(2015), 3326–3356. https://doi.org/10.1016/j.jfa.2015.01.001.Google Scholar
Tu, J.-L., La conjecture de Baum-Connes pour les feuilletages moyennables . K-Theory 17(1999), 215–264. https://doi.org/10.1023/A:1007744304422.Google Scholar
Yamashita, S., Cuntz’s ax + b-semigroup C∗-algebra over ℕ and product system C∗-algebras . J. Ramanujan Math. Soc. 24(2009), 299–322.Google Scholar
Yang, D., Endomorphisms and modular theory of 2-graph C∗-algebras . Indiana Univ. Math. J. 59(2010), 495–520. https://doi.org/10.1512/iumj.2010.59.3973.Google Scholar
Yang, D., Periodic k-graph algebras revisited . J. Aust. Math. Soc. 99(2015), 267–286. https://doi.org/10.1017/S1446788715000087.Google Scholar
Yang, D., The interplay between k-graphs and the Yang-Baxter equation . J. Algebra 451(2016), 494–525. https://doi.org/10.1016/j.jalgebra.2016.01.001.Google Scholar
Yang, D., Affine actions and the Yang–Baxter equation. arxiv:1607.03393.Google Scholar
Yeend, T., Groupoid models for the C∗-algebras of topological higher-rank graphs . J. Operator Theory 57(2007), 95–120.Google Scholar