Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T06:13:30.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundedness of Calderón–Zygmund Operators on Non-homogeneous Metric Measure Spaces

Published online by Cambridge University Press:  20 November 2018

Tuomas Hytönen ,
Suile Liu ,
Dachun Yang  and
Dongyong Yang
Tuomas Hytönen
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, Gustaf H¨allstr¨omin Katu 2B, Fi-00014 Helsinki, Finland email: tuomas.hytonen@helsinki.fi
Suile Liu
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex systems, Ministry of Education, Beijing 100875, People’s Republic of China email: slliu@mail.bnu.edu.cndcyang@bnu.edu.cn
Dachun Yang
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex systems, Ministry of Education, Beijing 100875, People’s Republic of China email: slliu@mail.bnu.edu.cndcyang@bnu.edu.cn
Dongyong Yang
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen 361005, People’s Republic of China email: dyyang@xmu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

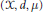Let $\left( \text{ }\!\!\chi\!\!\text{ ,}\,d,\,\mu \right)$ be a separable metric measure space satisfying the known upper doubling condition, the geometrical doubling condition, and the non-atomic condition that 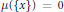$\mu \left( \left\{ x \right\} \right)\,=\,0$ for all 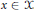$x\,\in \,\text{ }\!\!\chi\!\!\text{ }$. In this paper, we show that the boundedness of a Calderón–Zygmund operator 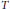$T$ on 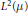${{L}^{2}}\left( \mu \right)$ is equivalent to that of 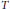$T$ on 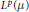${{L}^{p}}\left( \mu \right)$ for some 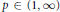$p\,\in \,\left( 1,\,\infty \right)$, and that of 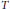$T$ from 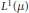${{L}^{1}}\left( \mu \right)$ to 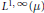${{L}^{1,\,\infty }}\left( \mu \right)$. As an application, we prove that if 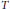$T$ is a Calderón–Zygmund operator bounded on 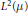${{L}^{2}}\left( \mu \right)$, then its maximal operator is bounded on 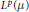${{L}^{p}}\left( \mu \right)$ for all 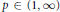$p\,\in \,\left( 1,\,\infty \right)$ and from the space of all complex-valued Borel measures on 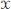$\text{ }\!\!\chi\!\!\text{ }$ to 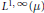${{L}^{1,\,\infty }}\left( \mu \right)$. All these results generalize the corresponding results of Nazarov et al. on metric spaces with measures satisfying the so-called polynomial growth condition.

Keywords

42B2042B2530L99upper doublinggeometrical doublingdominating functionweak type (1, 1) estimateCalderón–Zygmund operatormaximal operator
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 4 , 01 August 2012 , pp. 892 - 923
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Anh, B. T. and Duong, X. T., Hardy spaces, regularized BMO spaces and the boundedness of Calderon–Zygmund operators on non-homogeneous spaces. J. Geom. Anal., to appear.Google Scholar
[2] Bramanti, M., Singular integrals in nonhomogeneous spaces: L2 and Lp continuity from Hölder estimates. Rev. Mat. Iberoam. 26(2010), no. 1, 347–366.Google Scholar
[3] Coifman, R. R. and Weiss, G., Analyse harmonique non-commutative sur certains espaces homogènes. Lecture Notes in Math., 242, Springer-Verlag, Berlin-New York, 1971.Google Scholar
[4] Coifman, R. R. and Weiss, G., Extensions of Hardy spaces and their use in analysis. Bull. Amer. Math. Soc. 83(1977), no. 4, 569–645. http://dx.doi.org/10.1090/S0002-9904-1977-14325-5 Google Scholar
[5] Duoandikoetxea, J., Fourier analysis. Graduate Studies in Mathematics, 29, American Mathematical Society, Providence, RI, 2001.Google Scholar
[6] Grafakos, L., Classical Fourier analysis. Second ed., Graduate Texts in Mahematics, 249, Springer, New York, 2008.Google Scholar
[7] Grafakos, L., Modern Fourier analysis. Second ed., Graduate Texts in Mathematics, 250, Springer, New York, 2009.Google Scholar
[8] Heinonen, J., Lectures on analysis on metric spaces. Universitext, Springer-Verlag, New York, 2001.Google Scholar
[9] Hytönen, T., A framework for non-homogeneous analysis on metric spaces, and the RBMO space of Tolsa. Publ. Mat. 54(2010), no. 2, 485–504.Google Scholar
[10] Hytönen, T. and Martikainen, H., Non-homogeneous Tb theorem and random dyadic cubes on metric measure spaces. J. Geom. Anal., published online April 23, 2011. http://dx.doi.org/10.1007/s12220-011-9230-z Google Scholar
[11] Hytönen, T., Yang, Da., and Yang, Da., The Hardy space H 1 on non-homogeneous metric spaces. Math. Proc. Cambridge Philos. Soc., to appear.Google Scholar
[12] Mauceri, G. and Meda, S., BMO and H1 for the Ornstein-Uhlenbeck operator. J. Funct. Anal. 252(2007), no. 1, 278–313. http://dx.doi.org/10.1016/j.jfa.2007.06.017Google Scholar
[13] Nazarov, F., Treil, S., and Volberg, A., Weak type estimates and Cotlar inequalities for Calder´on-Zygmund operators on nonhomogeneous spaces.Internat. Math. Res. Notices 1998, no. 9, 463–487.Google Scholar
[14] Nazarov, F., Treil, S., and Volberg, A., The Tb-theorem on non-homogeneous spaces. Acta Math. 190(2003), no. 2, 151–239. http://dx.doi.org/10.1007/BF02392690Google Scholar
[15] Rudin, W. , Real and complex analysis. Third ed., McGram-Hill Book Co. New York, 1987.Google Scholar
[16] Tolsa, X. , BMO, H1, and Calderón–Zygmund operators for non doubling measures. Math. Ann. 319(2001), no. 1, 89–149. http://dx.doi.org/10.1007/PL00004432 Google Scholar
[17] Tolsa, X., Littlewood-Paley theory and the T (1) theorem with non-doubling measures. Adv. Math. 164(2001), no. 1, 57–116. http://dx.doi.org/10.1006/aima.2001.2011 Google Scholar
[18] Tolsa, X., Painlevé's problem and the semiadditivity of analytic capacity. Acta Math. 190(2003), no. 1, 105–149. http://dx.doi.org/10.1007/BF02393237 Google Scholar
[19] Volberg, A. and Wick, B. D., Bergman-type singular operators and the characterization of Carleson measures for Besov-Sobolev spaces on the complex ball. Amer. J. Math., to appear.Google Scholar