Article contents
Bounding the Iwasawa invariants of Selmer groups
Published online by Cambridge University Press: 29 June 2020
Abstract
We study the growth of p-primary Selmer groups of abelian varieties with good ordinary reduction at p in
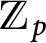 ${{Z}}_p$
-extensions of a fixed number field K. Proving that in many situations the knowledge of the Selmer groups in a sufficiently large number of finite layers of a
${{Z}}_p$
-extensions of a fixed number field K. Proving that in many situations the knowledge of the Selmer groups in a sufficiently large number of finite layers of a
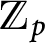 ${{Z}}_p$
-extension over K suffices for bounding the over-all growth, we relate the Iwasawa invariants of Selmer groups in different
${{Z}}_p$
-extension over K suffices for bounding the over-all growth, we relate the Iwasawa invariants of Selmer groups in different
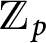 ${{Z}}_p$
-extensions of K. As applications, we bound the growth of Mordell–Weil ranks and the growth of Tate-Shafarevich groups. Finally, we derive an analogous result on the growth of fine Selmer groups.
${{Z}}_p$
-extensions of K. As applications, we bound the growth of Mordell–Weil ranks and the growth of Tate-Shafarevich groups. Finally, we derive an analogous result on the growth of fine Selmer groups.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
References
- 2
- Cited by



