Article contents
Bounds for the distribution of the Frobenius traces associated to products of non-CM elliptic curves
Published online by Cambridge University Press: 07 March 2022
Abstract
Let 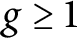 $g \geq 1$ be an integer and let
$g \geq 1$ be an integer and let 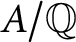 $A/\mathbb Q$ be an abelian variety that is isogenous over
$A/\mathbb Q$ be an abelian variety that is isogenous over 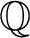 $\mathbb Q$ to a product of g elliptic curves defined over
$\mathbb Q$ to a product of g elliptic curves defined over 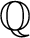 $\mathbb Q$, pairwise non-isogenous over
$\mathbb Q$, pairwise non-isogenous over 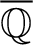 $\overline {\mathbb Q}$ and each without complex multiplication. For an integer t and a positive real number x, denote by
$\overline {\mathbb Q}$ and each without complex multiplication. For an integer t and a positive real number x, denote by 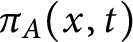 $\pi _A(x, t)$ the number of primes
$\pi _A(x, t)$ the number of primes 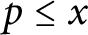 $p \leq x$, of good reduction for A, for which the Frobenius trace
$p \leq x$, of good reduction for A, for which the Frobenius trace 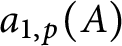 $a_{1, p}(A)$ associated to the reduction of A modulo p equals t. Assuming the Generalized Riemann Hypothesis for Dedekind zeta functions, we prove that
$a_{1, p}(A)$ associated to the reduction of A modulo p equals t. Assuming the Generalized Riemann Hypothesis for Dedekind zeta functions, we prove that 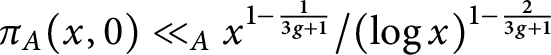 $\pi _A(x, 0) \ll _A x^{1 - \frac {1}{3 g+1 }}/(\operatorname {log} x)^{1 - \frac {2}{3 g+1}}$ and
$\pi _A(x, 0) \ll _A x^{1 - \frac {1}{3 g+1 }}/(\operatorname {log} x)^{1 - \frac {2}{3 g+1}}$ and 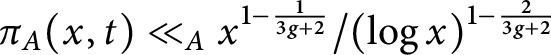 $\pi _A(x, t) \ll _A x^{1 - \frac {1}{3 g + 2}}/(\operatorname {log} x)^{1 - \frac {2}{3 g + 2}}$ if
$\pi _A(x, t) \ll _A x^{1 - \frac {1}{3 g + 2}}/(\operatorname {log} x)^{1 - \frac {2}{3 g + 2}}$ if 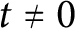 $t \neq 0$. These bounds largely improve upon recent ones obtained for
$t \neq 0$. These bounds largely improve upon recent ones obtained for 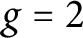 $g = 2$ by Chen, Jones, and Serban, and may be viewed as generalizations to arbitrary g of the bounds obtained for
$g = 2$ by Chen, Jones, and Serban, and may be viewed as generalizations to arbitrary g of the bounds obtained for 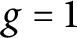 $g=1$ by Murty, Murty, and Saradha, combined with a refinement in the power of
$g=1$ by Murty, Murty, and Saradha, combined with a refinement in the power of 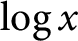 $\operatorname {log} x$ by Zywina. Under the assumptions stated above, we also prove the existence of a density one set of primes p satisfying
$\operatorname {log} x$ by Zywina. Under the assumptions stated above, we also prove the existence of a density one set of primes p satisfying 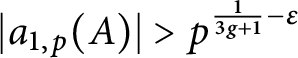 $|a_{1, p}(A)|>p^{\frac {1}{3 g + 1} - \varepsilon }$ for any fixed
$|a_{1, p}(A)|>p^{\frac {1}{3 g + 1} - \varepsilon }$ for any fixed 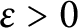 $\varepsilon>0$.
$\varepsilon>0$.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
A.C.C. was partially supported by a Collaboration Grant for Mathematicians from the Simons Foundation under Award No. 709008.
References
- 3
- Cited by


