Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T06:19:01.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Branching Rules for Ramified Principal Series Representations of GL(3) over a p-adic Field

Part of: Linear algebraic groups and related topics

Published online by Cambridge University Press:  20 November 2018

Peter S. Campbell  and
Monica Nevins
Peter S. Campbell
Affiliation:
Department of Mathematics, University of Bristol, UK, e-mail: peter.campbell@bristol.ac.uk
Monica Nevins
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, e-mail: mnevins@uottawa.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We decompose the restriction of ramified principal series representations of the 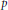$p$-adic group 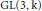$\text{GL}\left( 3,\,\text{k} \right)$ to its maximal compact subgroup 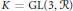$K\,=\,\text{GL}\left( 3,\,\mathcal{R} \right)$. Its decomposition is dependent on the degree of ramification of the inducing characters and can be characterized in terms of filtrations of the Iwahori subgroup in 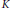$K$. We establish several irreducibility results and illustrate the decomposition with some examples.

Keywords

principal series representationsbranching rulesmaximal compact subgroupsrepresentations of p-adic groups

MSC classification

Secondary: 20G25: Linear algebraic groups over local fields and their integers 20G05: Representation theory
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 1 , 01 February 2010 , pp. 34 - 51
Copyright
Copyright © Canadian Mathematical Society 2010

References

[BO] U., Bader and U., Onn, On some geometric representations of GLn(O). arXiv:math/0404408v1.Google Scholar
[CN] P. S., Campbell and M., Nevins, Branching rules for unramified principal series representations of GL(3) over a p-adic field. J. Algebra 321(2009), no. 9, 2422-2444. doi:10.1016/j.jalgebra.2009.01.013Google Scholar
[GAP] The GAP Group, GAP - Groups, Algorithms, and Programming. Version 4.4, 2004. http://www.gap-system.org.Google Scholar
[Hi] G., Hill, On the nilpotent representations of GLn(O).Manuscripta Math. 82(1994), no. 3-4, 293-311. doi:10.1007/BF02567703Google Scholar
[H1] R. E., Howe, On the principal series of GLn over p-adic fields. Trans. Amer.Math. Soc. 177(1973), 275-286. doi:10.2307/1996596Google Scholar
[H2] R. E., Howe, Kirillov theory for compact p-adic groups. Pacific J. Math. 73(1977), no. 2, 365-381.Google Scholar
[L] G., Lusztig, Representations of reductive groups over finite rings. Represent. Theory 8(2004), 1-14. doi:10.1090/S1088-4165-04-00232-8Google Scholar
[N] M., Nevins, Branching rules for principal series representations of SL(2 over a p-adic field. Canad. J. Math. 57(2005), no. 3, 648-672.Google Scholar
[OPV] U., Onn, A., Prasad, and L., Vaserstein, A note on Bruhat decomposition of GL(n) over local principal ideal rings. Comm. Algebra 34(2006), no. 11, 4119-4130. doi:10.1080/00927870600876250Google Scholar
[P] V., Paskunas, Unicity of types for supercuspidal representations of GLN. >Proc. London Math. Soc. 91(2005), no. 3, 623-654. doi:10.1112/S0024611505015340Proc.+London+Math.+Soc.+91(2005),+no.+3,+623-654.+doi:10.1112/S0024611505015340>Google Scholar
[Si] A. J., Silberger, Irreducible representations of a maximal compact subgroup of pgl2 over the p-adics. Math. Ann. 229(1977), no. 1, 1-12. doi:10.1007/BF01420533Google Scholar