Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Deaconu, Valentin
and
Shultz, Fred
2006.
C*-algebras associated with interval maps.
Transactions of the American Mathematical Society,
Vol. 359,
Issue. 4,
p.
1889.
Arzumanian, V. A.
2007.
Operator algebras associated with polymorphisms.
Journal of Mathematical Sciences,
Vol. 140,
Issue. 3,
p.
354.
EXEL, R.
and
RENAULT, J.
2007.
Semigroups of local homeomorphisms and interaction groups.
Ergodic Theory and Dynamical Systems,
Vol. 27,
Issue. 6,
p.
1737.
Exel, R.
2007.
Interactions.
Journal of Functional Analysis,
Vol. 244,
Issue. 1,
p.
26.
EXEL, RUY
2008.
A new look at the crossed product of aC*-algebra by a semigroup of endomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 28,
Issue. 3,
p.
749.
Carlsen, Toke Meier
and
Silvestrov, Sergei
2009.
On the Exel Crossed Product of Topological Covering Maps.
Acta Applicandae Mathematicae,
Vol. 108,
Issue. 3,
p.
573.
Öinert, Johan
Silvestrov, Sergei
Theohari-Apostolidi, Theodora
and
Vavatsoulas, Harilaos
2009.
Commutativity and Ideals in Strongly Graded Rings.
Acta Applicandae Mathematicae,
Vol. 108,
Issue. 3,
p.
585.
BROWNLOWE, NATHAN
RAEBURN, IAIN
and
VITTADELLO, SEAN T.
2010.
Exel's crossed product for non-unital C*-algebras.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 149,
Issue. 3,
p.
423.
Thomsen, Klaus
2011.
On the C*-Algebra of a Locally Injective Surjection and its KMS States.
Communications in Mathematical Physics,
Vol. 302,
Issue. 2,
p.
403.
ANTONEVICH, A. B.
BAKHTIN, V. I.
and
LEBEDEV, A. V.
2011.
Ont-entropy and variational principle for the spectral radii of transfer and weighted shift operators.
Ergodic Theory and Dynamical Systems,
Vol. 31,
Issue. 4,
p.
995.
Laca, Marcelo
Raeburn, Iain
and
Ramagge, Jacqui
2011.
Phase transition on Exel crossed products associated to dilation matrices.
Journal of Functional Analysis,
Vol. 261,
Issue. 12,
p.
3633.
LUNDSTRÖM, PATRIK
and
ÖINERT, JOHAN
2012.
SKEW CATEGORY ALGEBRAS ASSOCIATED WITH PARTIALLY DEFINED DYNAMICAL SYSTEMS.
International Journal of Mathematics,
Vol. 23,
Issue. 04,
p.
1250040.
an Huef, Astrid
and
Raeburn, Iain
2012.
Stacey Crossed Products Associated to Exel Systems.
Integral Equations and Operator Theory,
Vol. 72,
Issue. 4,
p.
537.
BROWNLOWE, NATHAN
AN HUEF, ASTRID
LACA, MARCELO
and
RAEBURN, IAIN
2012.
Boundary quotients of the Toeplitz algebra of the affine semigroup over the natural numbers.
Ergodic Theory and Dynamical Systems,
Vol. 32,
Issue. 1,
p.
35.
Nystedt, Patrik
and
Öinert, Johan
2013.
Simple skew category algebras associated with minimal partially defined dynamical systems.
Discrete & Continuous Dynamical Systems - A,
Vol. 33,
Issue. 9,
p.
4157.
Cuntz, Joachim
and
Vershik, Anatoly
2013.
C*-Algebras Associated with Endomorphisms and Polymorphisms of Compact Abelian Groups.
Communications in Mathematical Physics,
Vol. 321,
Issue. 1,
p.
157.
Silvestrov, Sergei
2013.
Operator Algebra and Dynamics.
Vol. 58,
Issue. ,
p.
273.
ÖINERT, JOHAN
RICHTER, JOHAN
and
SILVESTROV, SERGEI D.
2013.
MAXIMAL COMMUTATIVE SUBRINGS AND SIMPLICITY OF ORE EXTENSIONS.
Journal of Algebra and Its Applications,
Vol. 12,
Issue. 04,
p.
1250192.
Hamada, Hiroyasu
2014.
Quotient Algebras of Toeplitz-Composition $$C^{*}$$ C ∗ -Algebras for Finite Blaschke Products.
Complex Analysis and Operator Theory,
Vol. 8,
Issue. 4,
p.
843.
Kwaśniewski, B. K.
2014.
Crossed Products for Interactions and Graph Algebras.
Integral Equations and Operator Theory,
Vol. 80,
Issue. 3,
p.
415.
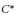 ${{C}^{*}}$-Algebras of Irreversible Dynamical Systems
${{C}^{*}}$-Algebras of Irreversible Dynamical Systems ${{C}^{*}}$-algebras which have been studied by, among others, Arzumanian, Vershik, Deaconu, and Renault, in connection with a measure-preserving transformation of a measure space or a covering map of a compact space, are special cases of the endomorphism crossed product construction recently introduced by the first named author. As a consequence these algebras are given presentations in terms of generators and relations. These results come as a consequence of a general theorem on faithfulness of representations which are covariant with respect to certain circle actions. For the case of topologically free covering maps we prove a stronger result on faithfulness of representations which needs no covariance. We also give a necessary and sufficient condition for simplicity.
${{C}^{*}}$-algebras which have been studied by, among others, Arzumanian, Vershik, Deaconu, and Renault, in connection with a measure-preserving transformation of a measure space or a covering map of a compact space, are special cases of the endomorphism crossed product construction recently introduced by the first named author. As a consequence these algebras are given presentations in terms of generators and relations. These results come as a consequence of a general theorem on faithfulness of representations which are covariant with respect to certain circle actions. For the case of topologically free covering maps we prove a stronger result on faithfulness of representations which needs no covariance. We also give a necessary and sufficient condition for simplicity.