Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T10:27:26.750Z Has data issue: false hasContentIssue false
  • English
  • Français

Canonical Resolution of a Quasi-ordinary Surface Singularity

Published online by Cambridge University Press:  20 November 2018

Chunsheng Ban  and
Lee J. McEwan
Chunsheng Ban
Affiliation:
Department of Mathematics, Ohio State University, U.S.A. email: cban@math.ohio-state.edu
Lee J. McEwan
Affiliation:
Department of Mathematics, Ohio State University, U.S.A. email: mcewan@math.ohio-state.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe the embedded resolution of an irreducible quasi-ordinary surface singularity 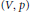$\left( V,\,p \right)$ which results from applying the canonical resolution of Bierstone-Milman to 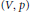$\left( V,\,p \right)$. We show that this process depends solely on the characteristic pairs of 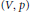$\left( V,\,p \right)$, as predicted by Lipman. We describe the process explicitly enough that a resolution graph for 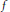$f$ could in principle be obtained by computer using only the characteristic pairs.

Keywords

14B0514J1732S0532S25canonical resolutionquasi-ordinary singularity
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 6 , 01 December 2000 , pp. 1149 - 1163
Copyright
Copyright © Canadian Mathematical Society 2000

References

[A] Abhyankar, S. S., Resolution of Singularities of Embedded Algebraic Surfaces. Springer Monographs in Math., 2nd Edition, 1998.Google Scholar
[BM1] Bierstone, E. and Milman, P., A simple constructive proof of canonical resolution of singularities. Effective Methods in Algebraic Geometry, Progr. Math. 94(1991), 11–30.Google Scholar
[BM2] Bierstone, E. and Milman, P., Resolution of singularities, (alg-geom/979028), preprint.Google Scholar
[BM3] Bierstone, E. and Milman, P., Canonical Desingularization in Characteristic Zero by Blowing Up theMaximum Strata of a Local Invariant. Invent. Math. 128(1997), 207–302.Google Scholar
[EV] Encinas, S. and Villamayor, O., Good points and algorithmic resolution of singularities Acta Math. 181(1998), 109–158.Google Scholar
[G] Gau, Y.-N., Embedded topological classification of quasi-ordinary singularities. Mem. Amer. Math. Soc. 74(1988), 109–129.Google Scholar
[H] Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero I, II. Ann. of Math. 79(1964), 109–326.Google Scholar
[L1] Lipman, J., Quasi-ordinary singularities of embedded surfaces. Ph.D. thesis, Harvard University, 1965.Google Scholar
[L2] Lipman, J., Quasi-ordinary singularities of surfaces in C3. Singularities, Proc. Symp. Pure Math. 40, Amer. Math. Soc. Providence 1983, Part 2, 161–171.Google Scholar
[L3] Lipman, J., Topological invariants of quasi-ordinary singularities. Mem. Amer. Math. Soc. 74(1988), 1–107.Google Scholar
[L4] Lipman, J., Equiresolution and Simultaneous Resolution of Singularities. Proceedings of Tirol Conference on Resolution of Singularities, to appear.Google Scholar
[M] Moh, T. T., Canonical uniformization of hypersurface singularities of characteristic zero. Comm. Algebra 20(1992) 3207–3251.Google Scholar
[O] Orbanz, U., Enbedded resolution of algebraic surfaces after Abhyankar (characteristic), Lecture Notes in Math. 1101, Springer, 1984.Google Scholar
[V1] Villamayor, O., Constructiveness of Hironaka's resolution. Ann. Sci. École Norm. Sup. (4) 22(1989), 1–32.Google Scholar
[V2] Villamayor, O., On Equiresolution and a Question of Zariski. preprint.Google Scholar