Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-15T02:15:28.552Z Has data issue: false hasContentIssue false
  • English
  • Français

Central Double Centralizers on Quasi-Central Banach Algebras with Bounded Approximate Identity

Published online by Cambridge University Press:  20 November 2018

Sin-Ei Takahasi
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We assume throughout this paper that A is a semi-simple, quasi-central, complex Banach algebra with a bounded approximate identity {eα}. The author [6] has shown that every central double centralizer T on A can be, under suitable conditions, represented as a bounded continuous complex-valued function ΦT on Prim A, the structure space of A with the hull-kernel topology, such that

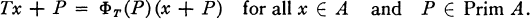
Here x + P for P ∊ Prim A denotes the canonical image of x in A/P. This map Φ is called Dixmier's representation of Z(M(A)), the central double centralizer algebra of A. We denote by τ the canonical isomorphism of A into the Banach algebra D(A) with the restricted Arens product as defined in [6]. Also denote by μ Davenport's representation of Z(M(A)). In fact, this map μ is given by

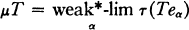
for each T ∊ Z(M(A)).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 2 , 01 April 1983 , pp. 373 - 384
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. R. J., Archbold, Density theorems for the center of a C*-algebra, J. London Math. Soc. (2) 10 (1975), 187–197.Google Scholar
2. J. W., Davenport, Multipliers on a Banach algebra with a bounded approximate identity, Pacific J. Math. 63 (1976), 131–135.Google Scholar
3. J., Dixmier, Les C*-algèbres et leurs représentations, Cahiers Scientifique 24 (Gauthier-Villars, Paris, 1964).Google Scholar
4. R., Larsen, The multiplier problem, Lecture Notes in Math. 105 (Springer-Verlag, Berlin, Heidelberg, New York, 1969).Google Scholar
5. C. E., Rickart, General theory of Banach algebras (Van Nostrand, N.J., 1960).Google Scholar
6. S., Takahasi, Dixmier's representation theorem of central double centralizers on Banach algebras, Trans. Amer. Math. Soc. 253 (1979), 229–236.Google Scholar
7. S., Takahasi, On the center of quasi-central Banach algebras with bounded approximate identity, Can. J. Math. 33 (1981), 68–90.Google Scholar
8. A. B., Willcox, Some structure theorems for a class of Banach algebras, Pacific J. Math. 6 (1956), 177–192.Google Scholar