Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T20:29:06.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Characteristic Cycles in Hermitian Symmetric Spaces

Published online by Cambridge University Press:  20 November 2018

Brian D. Boe  and
Joseph H. G. Fu
Brian D. Boe
Affiliation:
Department of Mathematics, University of Georgia, Athens, Georgia, USA 30602 e-mail: brian@math.uga.edu, fu@math.uga.edu
Joseph H. G. Fu
Affiliation:
Department of Mathematics, University of Georgia, Athens, Georgia, USA 30602 e-mail: brian@math.uga.edu, fu@math.uga.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give explicit combinatorial expresssions for the characteristic cycles associated to certain canonical sheaves on Schubert varieties X in the classical Hermitian symmetric spaces: namely the intersection homology sheaves IHX and the constant sheaves ℂX. The three main cases of interest are the Hermitian symmetric spaces for groups of type An (the standard Grassmannian), Cn (the Lagrangian Grassmannian) and Dn. In particular we find that CC(IHX) is irreducible for all Schubert varieties X if and only if the associated Dynkin diagramis simply laced. The result for Schubert varieties in the standard Grassmannian had been established earlier by Bressler, Finkelberg and Lunts, while the computations in the Cn and Dn cases are new.

Our approach is to compute CC(ℂX) by a direct geometric method, then to use the combinatorics of the Kazhdan-Lusztig polynomials (simplified for Hermitian symmetric spaces) to compute CC(IHX). The geometric method is based on the fundamental formula 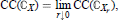where the Xr ↓ X constitute a family of tubes around the variety X. This formula leads at once to an expression for the coefficients of CC(ℂX) as the degrees of certain singular maps between spheres.

Keywords

14M1522E4753C65
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 49 , Issue 3 , 01 June 1997 , pp. 417 - 467
Copyright
Copyright © Canadian Mathematical Society 1997

References

[BB] Beilinson, A. and Bernstein, J., Localisation des G-modules, Comptes Rend. Acad. Sci. 292(1981), 15–18.Google Scholar
[Boe] Boe, B., Kazhdan-Lusztig polynomials for Hermitian symmetric spaces, Trans. Amer.Math. Soc. 309(1988), 279–294.Google Scholar
[BFL] Bressler, P., Finkelberg, M. and Lunts, V., Vanishing cycles in Grassmannians, Duke Math. J. 61(1990), 763–777.Google Scholar
[BDK] Brylinski, J.L., Dubson, A. and Kashiwara, M., Formule de l’indice pour les modules holonomes et obstruction d’Euler locale, Comptes Rend. Acad. Sci. 293(1981), 573–576.Google Scholar
[BK] Brylinski, J.L. and Kashiwara, M., Kazhdan-Lusztig conjecture and holonomic systems, Inv. Math. 64(1981), 378–410.Google Scholar
[Fe] Federer, H., Geometric measure theory, Springer-Verlag, New York, 1969.Google Scholar
[Fu1] Fu, J.H.G., Monge-Ampère functions I, Indiana U. Math. J. 38(1989), 745–771.Google Scholar
[Fu2] Fu, J.H.G., Curvature measures and Chern classes of singular varieties, J. Differential Geom. 39(1994), 251–280.Google Scholar
[Fu3] Fu, J.H.G., Curvature measures of subanalytic sets, Amer. J.Math. 116(1994), 819–880.Google Scholar
[Gin] Ginsburg, V., Characteristic varieties and vanishing cycles, Inv. Math. 84(1986), 327–402.Google Scholar
[Ha] Hardt, R., Slicing and intersection theory for currents associated to real analytic varieties, Acta Math. 129(1972), 57–136.Google Scholar
[Hel] Helgason, S., Differential Geometry, Lie Groups, and Symmetric Spaces, Academic Press, New York, 1978.Google Scholar
[KL1] Kazhdan, D. and Lusztig, G., Representations of Coxeter Groups and Hecke Algebras, Inv. Math. 53(1979), 165–184.Google Scholar
[KL2] Kazhdan, D., Schubert varieties and Poincarè duality, Proc. Symp. Pure Math. 36(1980), 185–203.Google Scholar
[KL3] Kazhdan, D., A topological approach to Springer's representations, Adv. Math. 38(1980), 222–228.Google Scholar
[Ka] Kashiwara, M., Private e-mail communication, July, 1995.Google Scholar
[KS] Kashiwara, M. and Schapira, P., Sheaves on manifolds, Springer-Verlag, 1992.Google Scholar
[KP] Kurdyka, K. and Parusiński, A., wf -stratification of subanalytic functions and the Łojasiewicz inequality, C. R. Acad. Sci. Paris Sr. I Math. 318(1994), 129–133.Google Scholar
[LS] Lascoux, A. and Schützenberger, M.-P., Polynômes de Kazhdan et Lusztig pour les Grassmanniennes, Astérisque 87–88(1981), 249–266.Google Scholar
[Mac] MacPherson, R., Chern classes for singular algebraic varieties, Ann. of Math. 100(1974), 423–432.Google Scholar
[Tak] Takeuchi, T., Cell decompositions and Morse equalities on symmetric spaces, J. Fac. Sci. Univ. of Tokyo, I 12(1965), 81–192.Google Scholar
[Tan] Tanisaki, T., Characteristic varieties of highest weight modules and primitive quotients, Adv. Studies in Pure Math. 14(1988), 1–30.Google Scholar