Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T01:55:46.415Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of Identities Implying Congruence Modularity I

Published online by Cambridge University Press:  20 November 2018

Alan Day  and
Ralph Freese
Alan Day
Affiliation:
Lakehead University, Thunder Bay, Ontario
Ralph Freese
Affiliation:
University of Hawaii, Honolulu, Hawaii
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

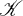In his thesis and [24], J. B. Nation showed the existence of certain lattice identities, strictly weaker than the modular law, such that if all the congruence lattices of a variety of algebras satisfy one of these identities, then all the congruence lattices were even modular. Moreover Freese and Jónsson showed in [10] that from this “congruence modularity” of a variety of algebras one can even deduce the (stronger) Arguesian identity.

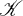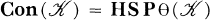These and similar results [3; 5; 9; 12; 18; 21] induced Jónsson in [17; 18] to introduce the following notions. For a variety of algebras , is the (congruence) variety of lattices generated by the class (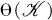) of all congruence lattices θ(A), 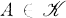. Secondly if is a lattice identity, and Σ is a set of such, 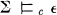holds if for any variety 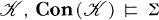implies .

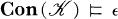Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 5 , 01 October 1980 , pp. 1140 - 1167
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Crawley, P. and Dilworth, R. P., Algebraic theory of lattices (Prentice-Hall, Englewood Cliffs, N.J., 1973).Google Scholar
2. Day, A., A characterization of modularity for congruence lattices of algebras, Can. Math. Bull. 12 (1969), 167–173.Google Scholar
3. Day, A., p-modularity implies modularity in equational classes, Algebra Universalis 3 (1973), 398–399.Google Scholar
4. Day, A., Lattice conditions implying congruence modularity, Algebra Universalis 6 (1976), 291–302.Google Scholar
5. Day, A., Splitting lattices and congruence modularity, Coll. Math. Soc. János Bolyai 17. Contributions to Universal Algebra, Szeged (1975), 57–71.Google Scholar
6. Day, A., Characterizations of finite lattices that are bounded-homomorphic images or sublattices of free lattices, Can. J. Math. 31 (1979), 69–78.Google Scholar
7. Dean, R. A., Component subsets of the free lattice on n generators, Proc. Amer. Math. Soc. 7 (1956), 220–226.Google Scholar
8. Freese, R., Minimal modular congruence varieties, Amer. Math. Soc. Notices 23 (1976).Google Scholar
9. Freese, R., The class of Arguesian lattices is not a congruence variety, Amer. Math. Soc. Notices 23 (1976).Google Scholar
10. Freese, R. and Jónsson, B., Congruence modularity implies the Arguesian identity, Algebra Universalis 6 (1976), 225–228.Google Scholar
11. Freese, R. and Nation, J. B., Congruence lattices of semilattices, Pacific J. Math. 49 (1973), 51–58.Google Scholar
12. Freese, R. and Nation, J. B., 3–3 lattice inclusions imply congruence modularity, Algebra Universalis 7 (1977), 191–194.Google Scholar
13. Gaskill, H. and Piatt, C., Sharp transferability and finite sublattices of a free lattice, Can. J. Math. 27 (1975), 1036–1041.Google Scholar
14. Hagemann, J. and Mitschke, A., On n-permutable congruences, Algebra Universalis 3 (1973), 8–12.Google Scholar
15. Hutchinson, G. and Czédli, Gábor, A test for identities satisfied in lattices of submodules, Algebra Universalis 8 (1978), 269–309.Google Scholar
16. Jónsson, B., Algebras whose congruence lattice is distributive, Math. Scad. 21 (1967), 110–121.Google Scholar
17. Jónsson, B., Varieties of algebras and their congruence varieties, Proceedings of the International Congress of Mathematicians, Vancouver (1974), 315–320.Google Scholar
18. Jóonsson, B., Identities in congruence varieties, Lattice Theory (Proc. Colloq. Szeged, 1974), Colloq. Math. Soc, János Bolyai 14 (1976), 195–205.Google Scholar
19. Jónsson, B. and Nation, J. B., A report on sublattices of a free lattice, Coll. Math. Soc. János Bolyai 17. Contributions to Universal Algebra, Szeged (1975).Google Scholar
20. Jonsson, B. and Rival, I., Lattice varieties covering the smallest non-modular variety, to appear.Google Scholar
21. Mederly, P., Three MaVcev type theorems and their applications, Math. Casopis Sloven. Akad. Vied. 25 (1975), 83–95.Google Scholar
22. McKenzie, R., Equational bases and non-modular lattice varieties, Trans. Amer. Math. Soc. 174 (1972), 1–43.Google Scholar
23. McKenzie, R., ome unresolved problems between lattice theory and equational logic, Proc. Houston Lattice Theory Conference (1973), 564–573.Google Scholar
24. Nation, J. B., Varieties whose congruences satisfy certain lattice identities, Algebra Universalis 4 (1974), 78–88.Google Scholar
25. Polin, S. V., On identities in congruence lattices of universal algebras, Mat. Zametki 22 (1977), 443–451. Translated in Mathematical Notes.Google Scholar
26. Taylor, W., Characterizing MaVcev conditions, Algebra Universalis 3 (1973), 351–397.Google Scholar
27. Wille, R., Kongruenzklassengeometrien, Lecture notes in mathematics 113 (Springer-Verlag, Berlin, 1970).CrossRefGoogle Scholar