A Characterization of the Quantum Cohomology Ring of G/B and Applications

Abstract

We observe that the small quantum product of the generalized flag manifold 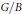$G/B$ is a product operation $\star $ on 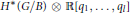${{H}^{*}}(G/B)\otimes \mathbb{R}\left[ {{q}_{1,...,}}{{q}_{l}} \right]$ uniquely determined by the facts that it is a deformation of the cup product on 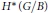${{H}^{*}}(G/B)$; it is commutative, associative, and graded with respect to deg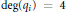$({{q}_{i}})=4$; it satisfies a certain relation (of degree two); and the corresponding Dubrovin connection is flat. Previously, we proved that these properties alone imply the presentation of the ring 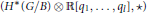$({{H}^{*}}(G/B)\otimes \mathbb{R}\left[ {{q}_{1,...,}}{{q}_{l}} \right]\star )$ in terms of generators and relations. In this paper we use the above observations to give conceptually new proofs of other fundamental results of the quantum Schubert calculus for 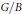$G/B$: the quantum Chevalley formula of D. Peterson (see also Fulton and Woodward) and the “quantization by standard monomials” formula of Fomin, Gelfand, and Postnikov for 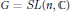$G=SL(n,\mathbb{C})$. The main idea of the proofs is the same as in Amarzaya–Guest: from the quantum 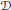$\mathcal{D}$-module of 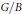$G/B$ one can decode all information about the quantum cohomology of this space.