Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-11T20:32:49.484Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizations of the Generalized Hughes Planes

Published online by Cambridge University Press:  20 November 2018

Heinz Lüneburg
Heinz Lüneburg*
Affiliation:
Universität Kaiserslautern, Kaiser slautern, Bundesrepublik Deutschland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 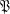be a projective plane and a subplane of 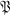. If l is a line of 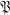, we let denote the group of all elations in that have as axis and leave Q invariant. In [12, p. 921], Ostrom asked for a description of all finite planes that have a Baer subplane with the property that for all lines l of . Here denotes the order of G. Both the desarguesian planes of square order and the generalized Hughes planes have this property (Hughes [10], Ostrom [14], Dembowski [6]). One of the aims of this paper is to show that these are the only planes having such a Baer subplane.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 2 , 01 April 1976 , pp. 376 - 402
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. André, J., Uber Perspektivitâten in endlichen projektiven Ebenen, Arch. Math. 6 (1954), 29–32.Google Scholar
2. Carter, R. W. and Fong, P., The Sylow 2-subgroups of the finite classical groups, J. Algebra 1, (1964), 139–151.Google Scholar
3. Daues, G.und Heineken, H., Dualitaten und Gruppen der Ordnung p5, to appear, Geometriae Dedicata.Google Scholar
4. Dembowski, P., Finite geometries (Springer Verlag, Berlin-Heidelberg-New York 1968).Google Scholar
5. Dembowski, P., Zur Géométrie der Gruppen PSL(3, q), Math. Z. 117 (1970), 125–134.Google Scholar
6. Dembowski, P., Generalized Hughes planes, Can. J. Math. 23 (1971), 481–494.Google Scholar
7. Dickson, L. E., Linear groups (Dover Publ. New York 1958).Google Scholar
8. Hering, Ch., On involutorial dations of projective planes, Math. Z. 132 (1973), 91–97.Google Scholar
9. Higman, D. G. and McLaughlin, J. E.,Geometric ABA-groups, 111. J. Math.5 (1961), 382–397.Google Scholar
10. Hughes, D. R., A class of non-Desarguesian projective planes, Can. J. Math. 9 (1957), 378–388.Google Scholar
11. Huppert, B., Endliche Gruppen I (Springer Verlag, Berlin-Heidelberg-New York 1967).Google Scholar
12. Lùneburg, H., Lectures on projective planes (Chicago 1969).Google Scholar
13. Ostrom, T. G., A characterization of the Hughes planes, Can. J. Math. 17 (1965), 916–922.Google Scholar
14. Ostrom, T. G., Vector spaces and construction of finite projective planes, Arch. Math. 19 (1968), 1–25.Google Scholar
15. Ostrom, T. G. and Wagner, A., On projective and affine planes with transitive collineation groups, Math. Z. 71 (1959), 186–199.Google Scholar
16. Prohaska, O., Endliche ableitbare affine Ebenen, Geometriae Dedicata 1 (1972), 6–17.Google Scholar
17. Rosati, L. A., I gruppi di collineazioni dei piani di Hughes, Boll. Un. Mat. Ital. 13 (1958), 505–513.Google Scholar
18. Rosati, L. A., Unicità e autodualità dei piani di Hughes, Rend. Sem. Mat. Univ. Padova 30 (1960), 316–327.Google Scholar
19. Rosati, L. A., Sui piani di Hughes generalizzati e i loro derivati, Le Matematiche 22 (1967), 289–302.Google Scholar
20. Schur, I., Uber die Darstellung der endlichen Gruppen durch gebrochen lineare Substitutionen, J. reine und angew. Math. 127 (1904), 20–50.Google Scholar
21. Schur, I., Untersuchungen uber die Darstellungen der endlichen Gruppen durch gebrochen lineare Substitutionen, J. reine und angew. Math. 132 (1907), 85–137.Google Scholar
22. Unkelbach, H., Eine Charakterisierung der endlichen Hughes-Ebenen, Geometriae Dedicata 1, (1973), 148–159.Google Scholar
23. Wagner, A., On perspectivities of finite projective planes, Math. Z. 71 (1959), 113–123.Google Scholar
24. Yaqub, J. C. D. S., Planes with given groups, To be published in the Proceedings of The Geometry Seminar which took place at Toronto in the summer of 1974.Google Scholar
25. Zassenhaus, H., Ùber endliche Fastkôrper, Abh. Hamburg 11, (1935), 187–220.Google Scholar