Published online by Cambridge University Press: 20 November 2018
Let R be a commutative ring with identity 1. A character of an R-algebra E is a homomorphism from E onto R, regarded as an algebra over itself. If (Eα) is a family of R-algebras indexed by a set A and if
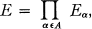
then for every β ∈ A and every character vβ of Eβ, vβ o prβ is a character of E where prβ is the projection homomorphism from E onto Eβ. Further if A is finite and if the only idempotents of R are 0 and 1 (equivalently, if R is not the direct sum of two proper ideals), it is easy to see that every character of E is of this form.