Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T10:44:27.235Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of Algebraic Surfaces withSectional Genus less than or Equal to Six.II: Ruled Surfaces with dim ϕKx⊗L(x) = l

Published online by Cambridge University Press:  20 November 2018

Elvira Laura Livorni
Elvira Laura Livorni*
Affiliation:
Instituto di Matematica, L'Aguila, Italy
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

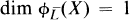Let L be a very ample line bundle on a smooth, connected, projective, ruled not rational surface X. We have considered the problem of classifying biholomorphically smooth, connected, projected, ruled, non rational surfaces X with smooth hyperplane section C such that the genus g = g(C) is less than or equal to six and dim where 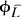is the map associated to 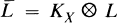. L. Roth in [10] had given a birational classification of such surfaces. If g = 0 or 1 then X has been classified, see [8].

If g = 2 ≠ hl,0(X) by [12, Lemma (2.2.2) ] it follows that X is a rational surface. Thus we can assume g ≦ 3.

Since X is ruled, h2,0(X) = 0 and

see [4] and [12, p. 390].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 5 , 01 October 1986 , pp. 1110 - 1121
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Andreotti, A. and Frankel, T, The Lefschetz theorem on hyperplane sections, Ann. of Math. 69 (1959), 713–717.Google Scholar
2. Baker, H. F., Principles of geometry, V (Cambridge University Press, 1933).Google Scholar
3. Bott, R., On a theorem of Lefschetz, Mich. Math. J. 6 (1959), 211–216.Google Scholar
4. Griffiths, P. A. and Harris, J., Principles of algebraic geometry (A. Wiley, Interscience, 1978).Google Scholar
5. Hartshorne, R., Algebraic geometry (Springer-Verlag, New York, 1977).CrossRefGoogle Scholar
6. Ionescu, P., An enumeration of all smooth projective varieties of degree 5 and 6, I.N.C.R.E.S.T. Preprint, Series in Mathematics 74 (1981).Google Scholar
7. Maruyama, M., On classification of ruled surfaces (Kinokuniya Bookstore Co. Ltd., Tokyo, Japan, 1970).Google Scholar
8. Nagata, M., On rational surfaces I, Mem. Coll. Sci. Kyoto (A) 32 (1960), 351–370.Google Scholar
9. Nagata, M., On self-intersection number of a section on a ruled surface, Nagoya Math. J. 37 (1970), 191–196.Google Scholar
10. Roth, L., On the projective classification of surfaces, Proc. London Math. Soc. (2) 42 (1937), 142–170.Google Scholar
11. Šafarevič, I. R., Algebraic surfaces, Proc. Steklov Inst. Math. 75 (1965), (translation by Amer. Math. Soc, 1967).Google Scholar
12. Sommese, A. J., Hyperplane sections of projective surfaces I — The adjunction mapping, Duke Math. J. Vol. 46 (1979).Google Scholar
13. Sommese, A. J., The birational theory of hyperplane sections of projective threefolds, preprint.Google Scholar
14. Ven, A. Van de, On the 2-connectedness of very ample divisors on a surface, Duke Math. J. 46 (1979), 403–407.Google Scholar