Article contents
Classification Theory and Stationary Logic
Published online by Cambridge University Press: 20 November 2018
Extract
Stationary logic L(aa) is obtained for Lωω by adding a quantifier aa which ranges over countable sets and is interpreted to mean “for a closed unbounded set of countable subsets”. The dual quantifier for aa is stat, i.e., stat sφ(s) is equivalent to ¬aa s ¬φ(s). In the study of the L(aa)-model theory of structures a particular well behaved class was isolated, the finitely determinate structures. These are structures in which the quantifier “stat” can be replaced by the quantifier “aa” without changing the validity of sentences. Many structures such as R and all ordinals are finitely determinate. In this paper we will be concerned with finitely determinate first order theories, i.e., those theories all of whose models are finitely determinate.
Example 0.1. [5] The theory of dense linear orderings is not finitely determinate. Let S be a stationary costationary subset of ω 1 and
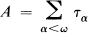
where
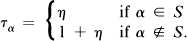
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1987
References
- 5
- Cited by

