Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-11T06:41:43.334Z Has data issue: false hasContentIssue false
  • English
  • Français

The Closure Ordering of Nilpotent Orbits of the Complex Symmetric Pair (SOp+q, SOp × SOq)

Published online by Cambridge University Press:  20 November 2018

Dragomir Ž. Ðoković  and
Michael Litvinov
Dragomir Ž. Ðoković
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, N2L 3G1 email: djokovic@uwaterloo.camichaellitvinov@rogers.com
Michael Litvinov
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, N2L 3G1 email: djokovic@uwaterloo.camichaellitvinov@rogers.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main problem that is solved in this paper has the following simple formulation (which is not used in its solution). The group 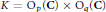$K={{O}_{p}}\left( C \right)\times {{O}_{q}}\left( C \right)$ acts on the space 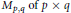${{M}_{p,\,q}}\,\text{of}\,p\,\times \,q$ complex matrices by 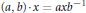$\left( a,b \right)\cdot x=ax{{b}^{-1}}$, and so does its identity component 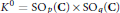${{K}^{0}}=\text{S}{{\text{O}}_{p}}\left( \text{C} \right)\times \text{S}{{\text{O}}_{\text{q}}}\left( \text{C} \right)$. A 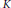$K$-orbit (or 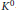${{K}^{0}}$-orbit) in 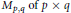${{M}_{p,q}}$ is said to be nilpotent if its closure contains the zero matrix. The closure, 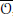$\bar{\mathcal{O}}$, of a nilpotent 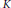$K$-orbit (resp. 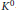${{K}^{0}}$-orbit) 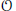$\mathcal{O}$ in 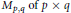${{M}_{p,q}}$ is a union of 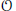$\mathcal{O}$ and some nilpotent 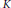$K$-orbits (resp. 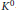${{K}^{0}}$-orbits) of smaller dimensions. The description of the closure of nilpotent 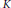$K$-orbits has been known for some time, but not so for the nilpotent 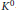${{K}^{0}}$-orbits. A conjecture describing the closure of nilpotent 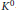${{K}^{0}}$-orbits was proposed in 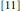$[11]$ and verified when 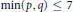$\min \left( p,\,q \right)\le 7$. In this paper we prove the conjecture. The proof is based on a study of two prehomogeneous vector spaces attached to 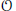$\mathcal{O}$ and determination of the basic relative invariants of these spaces.

The above problem is equivalent to the problem of describing the closure of nilpotent orbits in the real Lie algebra 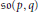$\mathfrak{s}\mathfrak{o}\left( p,\,q \right)$ under the adjoint action of the identity component of the real orthogonal group 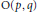$\text{O}\left( p,\,q \right)$.

Keywords

17B2017B4522E47orthogonalab-diagramsprehomogeneous vector spacesrelative invariants
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 6 , 01 December 2003 , pp. 1155 - 1190
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Barbasch, D. and Sepanski, M. R., Closure ordering and the Kostant.Sekiguchi correspondence. Proc. Amer. Math. Soc. 126(1998), 311–317.Google Scholar
[2] Collingwood, D. H. and McGovern, W. M., Nilpotent Orbits in Semisimple Lie Algebras. Van Nostrand, New York, 1992.Google Scholar
[3] Djoković, D. Ž., Closures of conjugacy classes in classical real linear Lie groups. In: Algebra (Carbondale, 1980), Lecture Notes in Math. 848, Springer-Verlag, Berlin and New York, 1981, 63–83.Google Scholar
[4] Djoković, D. Ž., Closures of conjugacy classes in classical real linear Lie groups, II. Trans. Amer. Math. Soc. 270(1982), 217–252.Google Scholar
[5] Djoković, D. Ž., The closure diagrams for nilpotent orbits of real forms of F 4 and G 2 . J. Lie Theory 10(2000), 491–510.Google Scholar
[6] Djoković, D. Ž., The closure diagrams for nilpotent orbits of real forms of E 6 . J. Lie Theory 11(2001), 381–413.Google Scholar
[7] Djoković, D. Ž., The closure diagrams for nilpotent orbits of the real forms E VI and E VII of E 7 . Represent. Theory 5(2001), 17–42.Google Scholar
[8] Djoković, D. Ž., The closure diagram for nilpotent orbits of the split real form of E 7 . Represent. Theory 5(2001), 284–316.Google Scholar
[9] Djoković, D. Ž., The closure diagram for nilpotent orbits of the real form E IX of E 8 . Asian J. Math. 5(2001), 561–584.Google Scholar
[10] Djoković, D. Ž., The closure diagram for nilpotent orbits of the split real form of E 8 . Preprint, 2002.Google Scholar
[11] Doković, D. Ž., Lemire, N. and Sekiguchi, J., The closure ordering of adjoint nilpotent orbits in so(p, q) . Tohoku Math. J. 53(2001), 395–442.Google Scholar
[12] Gyoja, A., Invariants, nilpotent orbits, and prehomogeneous vector spaces. J. Algebra 142(1991), 210–232.Google Scholar
[13] Kac, V. G., Some remarks on nilpotent orbits. J. Algebra 64(1980), 190–213.Google Scholar
[14] Mortajine, A., Classification des espaces préhomogènes de type parabolique réguliers et de leurs invariants relatifs. Hermann, Paris, 1991.Google Scholar
[15] Sato, M. and Kimura, T., A classification of irreducible prehomogeneous vector spaces and their relative invariants. Nagoya Math. J. 65(1977), 1–155.Google Scholar
[16] Sekiguchi, J., Remarks on real nilpotent orbits of a symmetric pair. J. Math. Soc. Japan 39(1987), 127–138.Google Scholar
[17] Vogan, D. A. Jr., The method of coadjoint orbits for real reductive groups. In: Representation Theory of Lie Groups (eds. Adams, J. and Vogan, D.), IAS/Park City Math. Ser. 8(2000), 179–238.Google Scholar