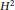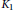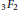Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ASAKURA, MASANORI
OTSUBO, NORIYUKI
and
TERASOMA, TOMOHIDE
2019.
AN ALGEBRO-GEOMETRIC STUDY OF SPECIAL VALUES OF HYPERGEOMETRIC FUNCTIONS .
Nagoya Mathematical Journal,
Vol. 236,
Issue. ,
p.
47.
Asakura, Masanori
and
Yabu, Toshifumi
2020.
Explicit logarithmic formulas of special values of hypergeometric functions 3F2.
Communications in Contemporary Mathematics,
Vol. 22,
Issue. 05,
p.
1950040.
Asakura, Masanori
2021.
Transcendence in Algebra, Combinatorics, Geometry and Number Theory.
Vol. 373,
Issue. ,
p.
1.