Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beineke, Lowell W.
1969.
The Many Facets of Graph Theory.
Vol. 110,
Issue. ,
p.
45.
Guy, Richard K.
1969.
The Many Facets of Graph Theory.
Vol. 110,
Issue. ,
p.
129.
Chartrand, Gary
Geller, Dennis
and
Hedetniemi, Stephen
1971.
Graphs with forbidden subgraphs.
Journal of Combinatorial Theory, Series B,
Vol. 10,
Issue. 1,
p.
12.
1973.
Graphs and Hypergraphs.
Vol. 6,
Issue. ,
p.
498.
Kozyrev, V. P.
1974.
Graph theory.
Journal of Soviet Mathematics,
Vol. 2,
Issue. 5,
p.
489.
Huang, Charlotte
1974.
On the existence of balanced bipartite designs, II.
Discrete Mathematics,
Vol. 9,
Issue. 2,
p.
147.
Hartman, Jehuda
1979.
Bounds on the Coarseness of the n-Cube.
Canadian Mathematical Bulletin,
Vol. 22,
Issue. 2,
p.
171.
Gross, Jonathan L.
and
Harary, Frank
1980.
Some problems in topological graph theory.
Journal of Graph Theory,
Vol. 4,
Issue. 3,
p.
253.
Guy, R. K.
and
Nowakowski, R. J.
1990.
Topics in Combinatorics and Graph Theory.
p.
297.
Adams, Peter
Bryant, Darryn
and
Buchanan, Melinda
2008.
A survey on the existence ofG‐Designs.
Journal of Combinatorial Designs,
Vol. 16,
Issue. 5,
p.
373.
Chimani, Markus
and
Gutwenger, Carsten
2009.
Non-planar core reduction of graphs.
Discrete Mathematics,
Vol. 309,
Issue. 7,
p.
1838.
Kolotoğlu, Emre
2013.
Decomposition of Complete Graphs into Isomorphic Complete Bipartite Graphs.
Journal of Combinatorial Designs,
Vol. 21,
Issue. 11,
p.
524.
Falconer, Kenneth J.
2022.
Richard Kenneth Guy, 1916–2020.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 1,
p.
318.
Huczynska, Sophie
and
Paterson, Maura B.
2024.
New Advances in Designs, Codes and Cryptography.
Vol. 86,
Issue. ,
p.
177.


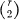 , but it has been shown (1) that
, but it has been shown (1) that