Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T22:24:09.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Coefficient Regions for Univalent Trinomials

Published online by Cambridge University Press:  20 November 2018

Q. I. Rahman  and
J. Waniurski
Q. I. Rahman
Affiliation:
Université de Montréal, Montréal, Québec
J. Waniurski
Affiliation:
Maria Curie-Sklodowska University, Lublin, Poland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem of determining necessary and sufficient conditions bearing upon the numbers a2 and a3 in order that the polynomial z + a2z2 + a3z3 be univalent in the unit disk |z| < 1 was solved by Brannan ([3], [4]) and by Cowling and Royster [6], at about the same time. For his investigation Brannan used the following result due to Dieudonné [7] and the well-known Cohn rule [9].

THEOREM A (Dieudonné criterion). The polynomial

1

is univalent in |z| < 1 if and only if for every Θ in [0, π/2] the associated polynomial

2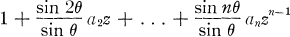

does not vanish in |z| < 1. For Θ = 0, (2) is to be interpreted as the derivative of (1).

The procedure of Cowling and Royster was based on the observation that 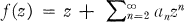is univalent in |z| < 1 if and only if for all α such that 0 ≧ |α| ≧ 1, α ≠ 1 the function

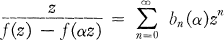
is regular in the unit disk.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 1 , 01 February 1980 , pp. 1 - 20
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Ahlfors, L. V., Complex analysis (McGraw-Hill, New York, 1966).Google Scholar
2. Bielecki, A. et Lewandowski, Z., Sur certaines familles de fonctions a-étoilées, Ann. Univ. Mariae Curie-Skfodowska, Sectio A. 15 (1961), 45–55.Google Scholar
3. Brannan, D. A., On univalent polynomials and related classes of functions, Thesis, University of London, 1967.Google Scholar
4. Brannan, D. A., Coefficient regions for univalent polynomials of small degree, Mathematik. 14 (1967), 165–169.Google Scholar
5. Copson, E. T., An introduction to the theory of functions of a complex variable (Oxford University Press, 1935).Google Scholar
6. Cowling, V. F. and Royster, W. C., Domains of variability for univalent polynomials, Proc. Amer. Math. Soc. 19 (1968), 767–772.Google Scholar
7. Dieudonné, J., Recherches sur quelques problèmes relatifs aux polynômes et aux fonctions bornées d'une variable complexe, Ann. Ecole Norm. Sup. (3. 48 (1931), 247–358.Google Scholar
8. Krzyz, J. and Rahman, Q. I., Univalent polynomials of small degree, Ann. Univ. Mariae Curie-Sklodowska, Sectio A. 21 (1967), 79–90.Google Scholar
9. Marden, M., Geometry of polynomials, Amer. Math. Soc. Math. Surveys, 3 (I960).Google Scholar
10. Pommerenke, Chr., Univalent functions (Vandenhoeck and Ruprecht, Gôttingen, 1975).Google Scholar
11. Rahman, Q. I. and Szynal, J., On some classes of polynomials, Can. J. Math. 30 (1978), 332–349.Google Scholar
12. Ruscheweyh, St. and Wirths, K. J., Uber die Koeffizienten spezieller schlichter Polynôme, Ann. Polon. Math. 28 (1973), 341–355.Google Scholar